Показательная функция, ее свойства и график

Функция вида y = a^x, где a больше нуля и а не равно единице называется показательной функцией. Основные свойства показательной функции:

1. Областью определения показательной функции будет являться множество вещественных чисел.

2. Область значений показательной функции будет являться множество всех положительных вещественных чисел. Иногда это множество для краткости записи обозначают как R+.

3. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0<a

4. Справедливы будет все основные свойства степеней. Основные свойства степеней представлены следующим равенствами:

a^x*a^y = a^{(x + y)};

(a^x)/(a^y) = a^(x-y);

(a*b)^x = (a^x)*(a^y);

(a/b)^x = a^x/b^x;

(a^x)^y = a^{(x * y)}.

Данные равенства будут справедливы для все действительных значений х и у.

5. График показательной функции всегда проходит через точку с координатами (0;1)

6. В зависимости от того возрастает или убывает показательная функция, её график будет иметь один из двух видов.

На следующем рисунке представлен график возрастающей показательной функции: a>0.

На следующем рисунке представлен график убывающей показательной функции: 0<a<1.

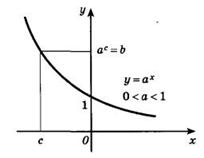
И график возрастающей показательной функции и график убывающей показательной функции согласно свойству, описанному в пятом пункте, проходят через точку (0;1).

7. Показательная функция не имеет точек экстремума, то есть другими словами, она не имеет точек минимума и максимума функции. Если рассматривать функцию на каком-либо конкретном отрезке, то минимальное и максимальное значения функция будет принимать на концах этого промежутка.

8. Функция не является четной или нечетной. Показательная функция это функция общего вида. Это видно и из графиков, ни один из них не симметричен ни относительно оси Оу, ни относительно начала координат.