Показательные неравенства. Основные способы решения.

Показательным неравенством называется неравенство, в котором неизвестная содержится только в показателе степени при постоянном основании А, А > 0, A ¹ 1.

При решении показательныx неравенств используются следующие утверждения:

A.1. Если a > 1, неравенство

a ^f(x) > a ^g(x)

равносильно неравенству

f(x) > g(x).

Аналогично, a ^f(x) < a ^g(x) Û f(x) < g(x).

A.2. Если 0 < a < 1, неравенство

a ^f(x) > a ^g(x)

равносильно неравенству

f(x) < g(x).

Аналогично, a ^f(x) < a ^g(x) Û f(x) > g(x).

A.3. Неравенство

[h(x)] ^f(x) > [h(x)] ^g(x)

равносильно совокупности систем неравенств

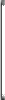
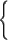
		h(x) > 1,
f(x) > g(x),
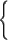
	0 < h(x) < 1,
f(x) < g(x).

Замечание.. Если знак неравенства (1) нестрогий, дополнительно рассматривается и случай

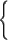
	h(x) = 1,
x Î D(f)Ç D(g),

где D(f) (D(g)) означает область определения функции f (g).

A.4. Если b ≥ 0, неравенство

a^f(x) < b

не имеет решений (следует из свойств показательной функции).

A.5. Если b ≤ 0, множеством решений неравенства a^f(x) > b является x Î D(f).

A.6. Если a > 1, b > 0, неравенство

a^f(x) > b

равносильно неравенству

f(x) > log_ab.

Аналогично, a ^f(x) < b Û f(x) < log_ab.

A.7. Если 0 < a < 1, b > 0, неравенство

a ^f(x) > b

равносильно неравенству

f(x) < log_ab.

Аналогично, a ^f(x) < b Û f(x) > log_ab.