
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Соотношения между тригонометрическими функциями одного аргумента
1. Выражение синуса через косинус
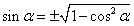
Примечание: Знак перед радикалом в правой части зависит от того, в какой четверти находитсяугол α. Знак тригонометрической функции в левой части должен совпадать со знаком правой части. Данное правило справедливо также для других формул, приведенных ниже.
2. Выражение синуса через тангенс
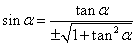
3. Выражение синуса через котангенс
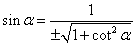
4. Выражение косинуса через синус
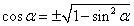
5. Выражение косинуса через тангенс
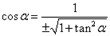
6. Выражение косинуса через котангенс
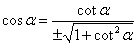
7. Выражение тангенса через синус
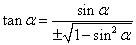
8. Выражение тангенса через косинус
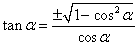
9. Выражение тангенса через котангенс
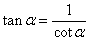
10. Выражение котангенса через синус
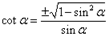
11. Выражение котангенса через косинус
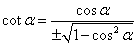
12. Выражение котангенса через тангенс
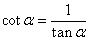
21. Тригонометрические функции y=sin x, y=cos x, их свойства и графики.
Y = sin(x)
График функции y=sin(x).
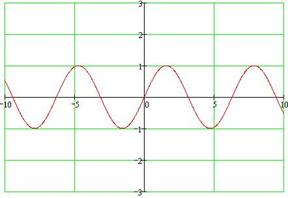
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
График функции y=cos(x).
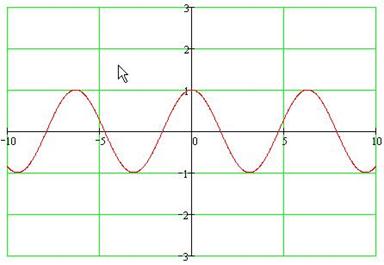
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция четная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
22. Тригонометрические функции y=tg x, y=ctg x, их свойства и графики.
График функции y=tg(x).
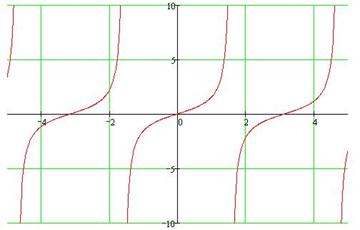
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
Y = ctg(x)
График функции y=ctg(x).
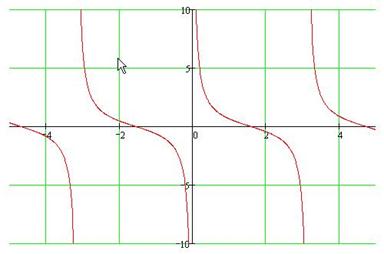
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
23. Основные свойства тригонометрических функций: четность, нечетность, периодичность. Знаки значений тригонометрических функций по четвертям.
Синусом числа а называется ордината точки, изображающей это число на числовой окружности. Синусом угла в а радиан называется синус числа а.
Синус - функция числа x. Ее область определения - множество всех чисел, так как у любого числа можно найти ординату изображающей его точки.
Область значений синуса - отрезок от -1 до 1, так как любое число этого отрезка на оси ординат является проекцией какой-либо точки окружности, но никакая точка вне этого отрезка не является проекцией какой-либо из этих точек.
Период синуса равен  . Ведь через каждые
. Ведь через каждые  положение точки, изображающей число, в точности повторяется.
положение точки, изображающей число, в точности повторяется.
Знак синуса:
1. синус равен нулю при  , где n - любое целое число;
, где n - любое целое число;
2. синус положителен при 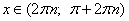 , где n - любое целое число;
, где n - любое целое число;
3. синус отрицателен при 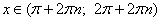
, где n - любое целое число.
Синус - функция нечетная. Во-первых, область определения этой функции есть множество всех чисел, а значит, 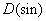 симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их ординаты - синусы - окажутся также противоположными. То есть
симметрична относительно начала отсчета. А во-вторых, если отложить от начала два противоположных числа: x и -x, то их ординаты - синусы - окажутся также противоположными. То есть 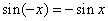 для любого x.
для любого x.
1. Синус возрастает на отрезках 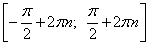 , где n - любое целое число.
, где n - любое целое число.
2. Cинус убывает на отрезке 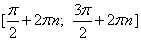 , где n - любое целое число.
, где n - любое целое число.
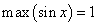 при
при 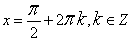 ;
;
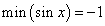 при
при 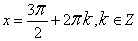 .
.
Дата добавления: 2015-04-18; просмотров: 350; Мы поможем в написании вашей работы!; Нарушение авторских прав |