Котангенс

Котангенсом числа называется отношение косинуса этого числа к синусу этого числа: 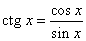. Котангенсом угла в а радиан называется котангенс числа а. Котангенс - функция числа. Ее область определения - множество всех чисел, у которых синус не равен нулю, так как никаких других ограничений в определении котангенса нет. И так как синус равен нулю при , то , где

Область значений котангенса - множество всех действительных чисел.

Период котангенса равен . Ведь если взять любые два допустимые значения x (не равные ), отличающиеся друг от друга на , и провести через них прямую, то эта прямая пройдет через начало координат и пересечет линию котангенсов в некоторой точке t. Вот и получится, что , то есть, что число является периодом котангенса.

Знак котангенса: котангенс - отношение косинуса к синусу. Значит, он

1. равен нулю, когда косинус равен нулю, то есть при .

2. положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при .

3. отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при .

Котангенс - функция нечетная. Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых, .

В силу нечетности синуса и четности косинуса, числитель полученной дроби равен , а ее знаменатель равен , а значит, сама эта дробь равна .

Вот и получилось, что . Котангенс убывает на каждом участке своей области определения, то есть на всех интервалах вида .