
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Преобразование произведения одноименных тригонометрических функций в сумму и разность
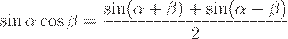 ,
,
 ,
,
 .
.
Первая формула получается сложением формул синуса суммы и синуса разности, в каждой из которых левую и правую часть поменяем местами:
 ,
,
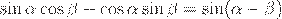 ,
,
 ,
,
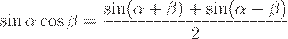 .
.
Вторая формула получается сложением, а третья — вычитанием следующих равенств (формул сложения для косинуса):
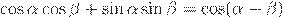 ,
,
 ,
,
 ,
,
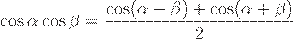 .
.
Окончательно:
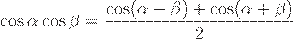 ,
,
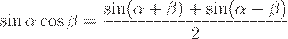 .
.
Применение этих формул иногда упрощает преобразование тригонометрического выражения.
29. Простейшие тригонометрические уравнения y=sin x, y=cos x, y=tg x, y=ctg x.
Уравнение sin x = a
Условия:
1) | a | ≤ 1
2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.
Формула решения уравнения sin x = a:
| x = (-1)n · arcsin α + πn где n – любое целое число (n ∈ Z). |
Частные случаи, когда уравнение sin x = а имеет более простое решение:
| Если… | То… |
| sin x = 0 | x = πn |
| sin x = 1 | x = π/2 +2πn |
| sin x = –1 | x = –π/2 +2πn |
Уравнение cos x = a
Условия:
1) | a | ≤ 1
2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.
Формула решения уравнения cos x = a:
| x = ± arccos α + 2πk где k – любое целое число (k ∈ Z). |
Частные случаи, когда уравнение cos x = а имеет более простое решение:
| Если… | То… |
| cos x = 0 | π x = — + πk 2 |
| cos x = 1 | x = 2πk |
| cos x = –1 | x = π + 2πk |
Уравнения tg x = a и ctg x = a.
Формула решения уравнения tg x = a:
| x = arctg a + πk где a – любое действительное число (a ∈R), k – любое целое число (k ∈ Z). |
Формула решения уравнения ctg x = a:
| x = arcctg a + πk где a – любое действительное число (a ∈R), k – любое целое число (k ∈ Z). |
Дата добавления: 2015-04-18; просмотров: 262; Мы поможем в написании вашей работы!; Нарушение авторских прав |