Тригонометрические функции суммы и разности двух аргументов (теоремы сложения)

Теорема1. Для любых действительных чисел α и β ( ) справедлива формула

(5.1)

Отметим, что в силу периодичности функции доказательство этой формулы достаточно провести для значений α и β, удовлетворяющих условиям: , .

Теорема 2. Для любых справедлива формула

(5.4)

Для доказательства достаточно воспользоваться формулой (5.1) и свойствами четности функции и нечетности функции :

Теорема 3. Для любых справедлива формула

(5.5)

Воспользуемся формулами приведения и формулой (5.1):

Теорема 4. Для любых справедлива формула

(5.6)

Доказательство. По формуле (5.5), используя свойства четности функции и нечетности функции , получаем:

Теорема 5. 1) Для любых 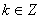, справедлива формула

(5.7)

2) Для любых 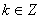, справедлива формула

(5.8)

3) Для любых 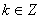, справедлива формула

(5.9)

4) Для любых 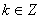, справедлива формула

(5.10)

Докажем формулу (5.7):