Закон электромагнитной индукции и его обобщение

Вопрос 1.

Согласно закону Фарадея в замкнутом проводнике, помещённом в магнитное поле, возникает ЭДС, пропорциональна скорости изменения магнитного потока, пронизывающего этот контур,

Обобщим этот закон, чтобы найти соотношение между и в точке пространства.

Учитывая, что ЭДС в замкнутом контуре , а магнитный поток, пронизывающий площадь , ограниченную контуром , получим из (1.26):

Наличие проводника позволяет лишь зафиксировать (обнаружить) ЭДС Таким образом, если имеем в пространстве переменное магнитное поле, то возникает и электрическое поле и они связаны соотношением

Интегрирование здесь ведётся по воображаемому контуру. Если будем рассматривать неподвижные среды, где магнитное поле меняется во времени, а контур фиксирован, то (1.27) можно переписать в виде:

При условии непрерывности подынтегральных функций и, сделав предельный переход, аналогично, как в выражении (1.18) получим

Это дифференциальная форма закона электромагнитной индукции, связывающая и , в точке пространства. Подчеркнём, что из обобщений Максвелла вытекает исключительно важное представление о физической природе поля.

Существование электрического поля связано не только с наличием электрических зарядов, но для его возникновения также достаточно только изменения во времени магнитного поля.

Из (1.29) находим, что

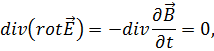
так как 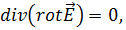т. е. поэтому всегда Перестановка оператора и допустима, так как по предложению в обыкновенной точке поля вектор непрерывен со всеми своими производными.

Из постоянства дивергенции в любой точке поля следует, что если когда-либо в прошлом поле отсутствовало (т. е. было время, когда 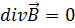), то и всегда Утверждение о том, что всегда находится в соответствии со сделанным ранее указанием на соленоидальность поля вектора , вследствие отсутствия истинного магнетизма (магнитных масс).