Закон сохранения электрического заряда

Согласно лежащему в основе теории электричества закону сохранения электрического заряда, электрические заряды не могут ни возникать, ни исчезать, они лишь могут перемещаться в пространстве.

Если рассматривается какая-либо замкнутая система, то количества отрицательных и положительных зарядов сохраняются постоянными и изменение электрического состояния системы сводится лишь к перераспределению этих зарядов в пространстве.

Рис. 1.3

Если из какого-либо объёма вытекает электрический ток (рис. 1.3), внутри заряд уменьшается, т. е.

Формула (1.8) представляет собой интегральное выражение закона сохранения электрического заряда.

От интегральной формы перейдём к дифференциальной. Если внутри объёма заряд распределён с объёмной плотностью , то Учитывая это из (1.8) имеем

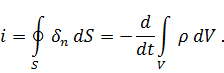
Следовательно,

Выражение (1.9) справедливо при сколь угодно малом объёме . Для конечного объёма можно записать

Эта формула будет точной, если . Возьмём предел отношения

Этот предел может быть вычислен и в математике, он называется дивергенцией (расхождением) вектора и обозначается , т. е.

Из курса математики известно, что вектора в прямоугольной системе координат вычисляется следующим образом:

Таким образом, получим:

Выражение (1.10) представляет дифференциальную форму закона сохранения электрического заряда. Эту формулу также называют уравнением непрерывности ( и должны удовлетворять условиям конечности и непрерывности в любой точке рассматриваемой области).

В (1.9) заменим по формуле (1.10), получим

Это выражение есть формула Остроградского. Она является общей формулой преобразования поверхностного интеграла в объёмный и справедлива для любого вектора, который непрерывен вместе со своими производными во всех точках объёма и на ограничивающей его поверхности .

Если в каждой точке определённой области плотность заряда постоянна во времени, т. е. , то ток, входящий в эту область через ограничивающую замкнутую поверхность , должен быть всё время равен току, выходящему наружу. В этом случае из (1.9) имеем:

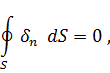
а из (1.10) следует, что . Если функции, описывающие процесс, не зависят от времени, то такой процесс, как известно, называется стационарным.

Таким образом, стационарное течение электричества определяется вектором , который в каждой точке области постоянен по величине и направлению. Так как распределения стационарного тока всюду равна нулю, то в стационарном состоянии все линии тока замкнуты сами на себя. Иными словами, поле вектора при постоянном токе является соленоидальным.

Рассмотренный здесь ток представляет движение электрических зарядов. Поскольку среды, в которых наблюдается движение электрических зарядов, называются проводящими, то рассмотренный нами ток называется током проводимости.

4 вопрос