Ток смещения. Уравнения Максвелла

Стационарное (постоянное) электромагнитное поле – такое поле, которое с течением времени не меняется, т. е. Соберём все результаты, которые получили ранее, полагая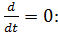

а) ;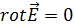

в) ;

г) ;

д)

При этом уравнение д) находится в полном соответствии с уравнением б), так как =0. Данные уравнения не имеют внутренних противоречий [6].

Переменное электромагнитное поле. В этом случае 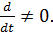Уравнения а) и д) из (1.30) запишутся следующим образом:

Если предположить, что уравнения б), в) и г) сохраняются и для переменного электромагнитного поля, то заметим, что уравнение а) совместимо с уравнением в); уравнение д) противоречит уравнению б). Следовательно, уравнение д) справедливо для постоянного тока, не справедливо для переменного тока.

Максвелл устранил это противоречие введением нового понятия – тока смещения и соответствующим обобщением закона полного тока.

Подставляя значение в уравнение 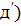из уравнения г), получим:

Следовательно,

Таким образом, получили, что уже не , а всегда равна 0. Максвелл назвал вектором плотности тока смещения , т. е.

(1.32)

Обозначим

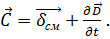
Вектор называется вектором объёмной плотности полного тока.

Причём всегда выполняется условие соленоидальности вектора :

В проводящей среде при изменяющемся во времени электромагнитном поле должны наблюдаться оба тока – ток проводимости и ток смещения. Следовательно, для переменного электромагнитного пол уравнение б) запишется более общим уравнением

При наличии же сторонних ЭДС нужно к добавить .

Таким образом, Максвелл составил наиболее общую систему уравнений переменного (нестационарного) электромагнитного поля, которая справедлива для стационарного поля, положив в ней :

Уравнения (1.35) и есть уравнения Максвелла, которые лежат в основе теории электромагнитного поля. Из них уравнения – основные, уравнения и 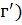– их следствия, уравнение – уравнение непрерывности или дифференциальная форма закона сохранения электрического заряда. Заметим, что уравнения (1.30) для постоянного поля являются частным случаем уравнений (1.35).

Универсальность уравнений Максвелла заключается в том, что они не содержат никаких сред. Исключительно симметричный вид принимают уравнения (1.35) в случае идеального ( 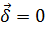) и незаряженного ( =0) диэлектрика (например, вакуум):

В этих уравнениях положено, что . Уравнения (1.36) можно применять во многих случаях и к реальным диэлектрикам, например, к воздуху. Уравнение соответствует тому, что переменное магнитное поле порождает электрическое поле. Уравнение соответствует тому, что переменное электрическое поле порождает магнитное поле.

Уравнения (1.36) дают отличные от нуля решения. Следовательно, может существовать электромагнитное поле независимо от его источника. Такое электромагнитное поле может быть только переменным. Это электромагнитное поле называется электромагнитными волнами.

Вопрос 5.