Переменное электромагнитное поле. Запаздывающие потенциалы

Переменное электромагнитное поле характеризуется известными нам тремя уравнениями (1.66 – 1.68). В случае переменного электромагнитного поля нет возможности разделить магнитное поле от электрического. Это процесс взаимосвязанный. При решении необходимо знать либо сторонние токи, либо сторонние заряды, начальные и граничные условия.

Если имеем однородное безграничное пространство, то нам нужно знать только токи и заряды. На практике этот случай редок, но он имеет фундаментальное значение.

Рассмотрим этот случай для среды без потерь, т. е. при уравнения (1.66 – 1.68) примут вид:

^.

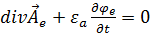Уравнение (1.70) может быть записано в виде трёх скалярных уравнений в прямоугольной системе координат. В результате имеем:

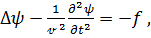
где – проекции или функции ;

– означает 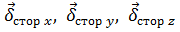или ;

– имеет размерность скорости.

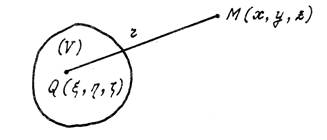
Рис. 1.13

Уравнение (1.72) есть неоднородное волновое уравнение. Частным решением его является

где – объём области пространства, в котором задана функция (рис. 1.13);

– точка, находящаяся в объёме , в ней расположен источник поля;

– время, предшествующее времени 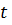на величину ;

– время запаздывания, которое необходимо, чтобы процесс распространялся от точки до точки .

Данный потенциал определяется поведением источников в момент времени . Потенциалы в силу наличия времени запаздывания называются запаздывающими. В результате для электрического вектор-потенциала и скалярного потенциала получим:

Формулы (1.74) и (1.75) находят широкое применение для расчёта изучения антенн, когда токи в них заданы.