
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вектор-потенциал и скалярный потенциал
Для облегчения решений уравнений Максвелла вводятся вспомогательные функции: вектор-потенциал и скалярный потенциал. Одним из уравнений Максвелла, которое всегда выполняется, является
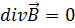 .
.
Это уравнение будет тождественно удовлетворяться, если положить
 так как
так как 
где  – новый пока произвольный непрерывный и имеющий производные вектор.
– новый пока произвольный непрерывный и имеющий производные вектор.
Вектор 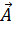 называется вектор-потенциалом и широко применяется в общих исследованиях электромагнитного поля.
называется вектор-потенциалом и широко применяется в общих исследованиях электромагнитного поля.
Ограничимся рассмотрением сред, когда 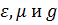 являются постоянными, т. е. среда – изотропная, однородная. В этом случае
являются постоянными, т. е. среда – изотропная, однородная. В этом случае
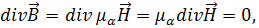 т. е.
т. е. 
Следовательно, для изотропной однородной среды не только
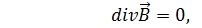 но и
но и 
|
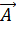 вводится вектор
вводится вектор  :
:

Так как  то
то  т. е. мы получаем электрический вектор-потенциал.
т. е. мы получаем электрический вектор-потенциал.
Заметим, что как  , так и вектор
, так и вектор  определяются неоднозначно.
определяются неоднозначно.
Действительно, если имеем поле вектора  , то оно может быть представлено в виде
, то оно может быть представлено в виде
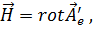
где  так как
так как 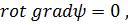
где  – скалярная произвольная непрерывная функция, имеющая производные.
– скалярная произвольная непрерывная функция, имеющая производные.
Из курса математики известно, что результатом градиента является вектор, который определяется следующим образом:

а модуль этого вектора определяется:

Следовательно, если мы нашли вектор  , удовлетворяющий уравнению (1.59), то всякий другой вектор
, удовлетворяющий уравнению (1.59), то всякий другой вектор  тоже удовлетворяет уравнению (1.59).
тоже удовлетворяет уравнению (1.59).
Однако эта неоднозначность в определении вектора  делает его удобным для вычислений, так как мы можем наложить ряд условий на вектор-потенциал, чтобы упростить вычисления.
делает его удобным для вычислений, так как мы можем наложить ряд условий на вектор-потенциал, чтобы упростить вычисления.
Чему должен удовлетворять вектор-потенциал 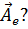
Из первого уравнения Максвелла
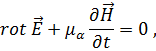
используя уравнение (1.59), получим:
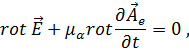
т. е.

Полученное уравнение будет выполняться при условии, если
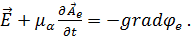 ,
,
так как 
где  – произвольная скалярная функция, которая называется электрическим скалярным потенциалом.
– произвольная скалярная функция, которая называется электрическим скалярным потенциалом.
Знак минус выбран потому, что данное уравнение должно выполняться и для постоянного поля, когда  . В этом случае получаем
. В этом случае получаем

т. е. известное из курса физики положение, что напряжённость электрического поля есть минус градиент потенциала.
Следовательно,
|
 .
.
Определим условия, которым должны удовлетворять  и
и  . Для этого используем второе уравнение Максвелла
. Для этого используем второе уравнение Максвелла

Если в этом уравнении заменить 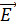 и
и 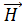 по формулам (1.60) и (1.61), то получим:
по формулам (1.60) и (1.61), то получим:
|
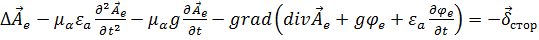 .
.
Напомним, что
 – оператор Лапласа или лапласиан. Это скалярный дифференциальный оператор второго порядка;
– оператор Лапласа или лапласиан. Это скалярный дифференциальный оператор второго порядка;

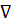 – оператор Гальмитона или набла. Это векторный дифференциальный оператор первого порядка:
– оператор Гальмитона или набла. Это векторный дифференциальный оператор первого порядка:
|
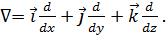
Теперь используем третье уравнение Максвелла
 или
или 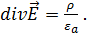
Применяя формулу (1.61) , получим:

Но

Следовательно,

Теперь имеем скалярные уравнения (1.62) и (1.63). Правая часть этих уравнений проста. Однако уравнение (1.62) очень громоздко. Но если использовать неоднозначность определения  , уравнение упрощается, а именно: налагается дополнительное условие в виде
, уравнение упрощается, а именно: налагается дополнительное условие в виде  . Это равенство называется уравнением связи. Отсюда
. Это равенство называется уравнением связи. Отсюда
|
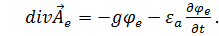
Подставив (1.64) в уравнение (1.63), получим
|
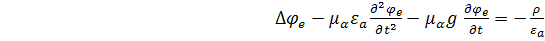 .
.
Соберём полученные результаты:
|

|
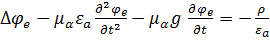 .
.
При условии
|
 .
.
При этом векторы 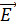 и
и  определяются по формулам
определяются по формулам
|
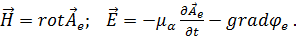
Уравнение (1.68) называется уравнением связи или калибровочным уравнением. Из данных выражений следует, что решение задачи об электромагнитном поле сводится к решению типового уравнения (1.66) или (1.67) при условии выполнения (1.68). Векторы 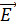 и
и  определяются по формулам (1.69).
определяются по формулам (1.69).
Уравнения (1.66) и (1.67) относятся к известным уравнениям математики – типовым волновым неоднородным уравнениям. Решения этих уравнений разработаны. Совокупное решение (1.66 – 1.69) будет единственно возможным, если оно будет удовлетворять начальным и граничным условиям поставленной физической задачи.
Вопрос 9.
1.10. Волновые уравнения для векторов 
Рассмотрим волновые уравнения для случая однородной, изотропной среды. Даны уравнения Максвелла:

|

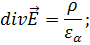
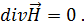
Задача заключается в решении уравнений Максвелла. Преобразуем уравнения (1.57) таким образом, чтобы получить отдельно уравнение для  и отдельно уравнение для
и отдельно уравнение для  [1,6]. Для этого возьмём
[1,6]. Для этого возьмём 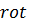 от первого уравнения и, используя второе уравнение, получим:
от первого уравнения и, используя второе уравнение, получим:
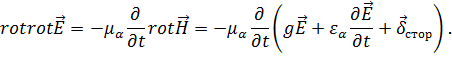
Учитывая, что  соберём все члены, содержащие
соберём все члены, содержащие 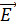 в левую часть, получим:
в левую часть, получим:
 (1.58)
(1.58)
Аналогично для  . Возьмём
. Возьмём 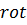 от второго уравнения и, используя первое, получим:
от второго уравнения и, используя первое, получим:
|
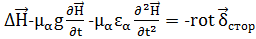
Уравнение (1.58) есть волновое уравнение для вектора  , а (1.59) – волновое уравнение для вектора
, а (1.59) – волновое уравнение для вектора  .
.
Правые части уравнений (1.58) и (1.59), которые выражаются через заданные функции  и
и  , достаточно сложны. Непосредственное решение уравнений (1.58) и (1.59) встречает большие трудности. Для того чтобы облегчить решение этих уравнений, вводятся вспомогательный вектор и функция, так называемые электродинамические потенциалы. При этом уменьшается число уравнений, правая часть их упрощается. После определения вспомогательных функций и определения через них
, достаточно сложны. Непосредственное решение уравнений (1.58) и (1.59) встречает большие трудности. Для того чтобы облегчить решение этих уравнений, вводятся вспомогательный вектор и функция, так называемые электродинамические потенциалы. При этом уменьшается число уравнений, правая часть их упрощается. После определения вспомогательных функций и определения через них  и
и  , не нужно устанавливать соответствие между ними.
, не нужно устанавливать соответствие между ними.
Вспомогательными функциями бывают вектор-потенциал и скалярный потенциал, а также вектор Герца.
Вопрос 10.
Дата добавления: 2015-04-18; просмотров: 281; Мы поможем в написании вашей работы!; Нарушение авторских прав |