Силы, действующие в жидкости. Гидростатическое давление

В гидростатике изучается теория равновесия жидкостей и газов. Для выяснения условий равновесия необходимо рассмотреть силы, действующие на некоторый объем жидкости. Существует много различных принципов классификации сил, приложенных к частицам сплошных сред. В зависимости от обла­сти приложения силы делятся на внутренние и внешние. По своей природе или по характеру действия силы делятся на массовые (или объемные) и поверхностные.

Массовые, или объемные, силы пропорциональны массе выде­ленного объема или при постоянной плотности среды пропорцио­нальны объему, они действуют на все частицы среды этого объема. Массовыми силами являются силы веса, все электромагнит­ные объемные силы, в том числе силы Лоренца и силы элек­тростатического напряжения, и различные силы инерции (Кориолисова сила, центробежная сила и др.).

Поверхностные силы действуют лишь на поверхность выделен­ного объема. Обычно поверхностные силы складываются из по­верхностных сил, направленных по нормали к выделенной пло­щадке и поверхностных сил, направленных по касательной к этой площадке.

В покоящейся жидкости поверхностные силы направлены по нормали к элементу поверхности выделенного объема. В движущейся вязкой жидкости имеют место и нормальные, и касательные составляющие поверхностных сил. Последние определяют силы трения.

Распределение массовых сил в некотором объеме DV задается вектором плотности массовой силы, равным пределу отношения главного вектора массовых сил 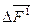, приложенных к частицам некоторого объема с массой Dm, к этой массе при стремлении последней к нулю.

Для характеристики распределения массовых сил обычно пользуются осредненным значением вектора плотности массовых сил, равным отношению главного вектора массовых сил к вели­чине массы, т. е.

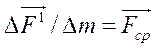
Размерность плотности массовой силы совпадает с размерностью ускорения.

В отличие от объемных сил, вектор которых для частицы среды определяется однозначно, величина поверхностной силы в точке в общем случае зависит от выбора направления элементарной площадки.

Обычно рассматриваются не сами поверхностные силы, а их напряжения, т. е.

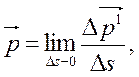
где 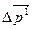— главный вектор поверхностных сил, приложенных

к некоторой площадке Ds.

Размерность напряжений будет

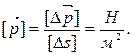
В практике давление измеряется следующими единицами:

· Паскаль (принято в системе СИ, основная единица измерения давления по ГОСТ РФ); Па = [Ньютон / м²].

· Бар (единица, принятая в Европе); 1 bar = 0,1 МПа.

· Миллиметр ртутного столба.

· Метр водяного столба.

· Фунт – сила на квадратный дюйм – psi (единица, принятая в Северной Америке); 1 psi = 52,2 мм рт. ст.

· Килограмм-сила на квадратный сантиметр (единица измерения давления, широко применяемая ранее в СССР); 1 bar = 1, 02 кгс/ см².

Рассмотрим условие равновесия элементарного жидкого объ­ема, находящегося под действием поверхностных и массовых сил.

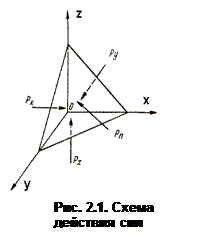
Для этого в покоящейся жидкости выделим некоторый элемен­тарный тетраэдр с длиной ребер dx, dy, dz (рис. 2.1). Три грани тетраэдра лежат в координатных плоскостях, а четвертая — на­клонная грань — является замы­кающей. Пусть площади соответ­ствующих граней будут s_x, s_y, s_z и s_n.

Поверхностные силы элементар­ного тетраэдра пропорциональны произведению двух длин сторон тетраэдра, а массовые - объему. Следовательно, массовыми силами как величинами третьего порядка малости можно пренебречь по сравнению с поверхностными си­лами — величинами второго по­рядка малости.

Согласно основному свойству жидкостей, находящихся в рав­новесии, поверхностные силы, заменяющие действие отброшенной части жидкости при выделении тетраэдра, будут направлены по нормали к граням тетраэдра. Таким образом, эти силы являются силами давления. Если обозначить величины сил давления, при­ложенных к граням P_х, Р_у, P_z и P_n (рис. 2.1), то для сохранения условий равновесия, известных из статики твердого тела, необ­ходимо, чтобы сумма всех внешних сил или сумм проекций всех внешних сил на координатные оси была равна нулю. Для рас­сматриваемого тетраэдра это условие можно записать в виде:

,

,

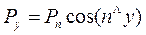где п — орт нормали к наклонной грани.

Если первое уравнение системы разделим на величину пло­щадки s_x, а второе и третье соответственно на s_y и s_z;, то получим условие равновесия в величинах напряжений сил давления: , ,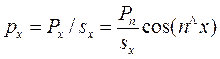

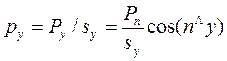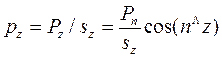
Но из рис. 2.1 видно, что s_x, s_y и s_z — проекции наклонной грани соответственно на плоскости у0z, хОz и хОу, т. е.

,

,

.

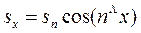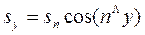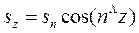Подставив эти величины в правые части предшествующих уравнений, окончательно получим

p_x=p_n; p_y=p_n; p_z=p_n

или p_x= p_y= p_z=p_n=р (2.1)