Равновесие тяжелой несжимаемой жидкости

Для несжимаемой тяжелой жидкости при отсутствии других массовых сил, кроме сил тяжести, имеем (ось z направлена вертикально вниз) X=Y=0 и Z=g, уравнения равновесия (2.2) в этом случае принимают вид:

,

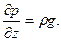
Первые два из этих уравнений выражают независимость да­вления от координат х и у, т. е. поверхностями равного давления или поверхностями уровня являются горизонтальные плоскости. Интегрирование третьего уравнения

(2.7)

при постоянных значениях g и r приводит к результату

. (2.8)

Если начало координат поместить на свободную поверхность покоящейся жидкости, на которой постоянное давление р₀ задано или для открытого сосуда равно атмосферному давлению, то, как следует из выражения (2.8), при z= 0, С = р_о. Подставив значение постоянной С в уравнение (2.8) и имея в виду, что pg = g (g - удельный вес жидкости), окончательно получим величину гидростатического давления в виде

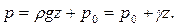(2.9)

Это соотношение является выражением общего гидростатиче­ского закона, который формулируется следующим образом:

давление в любой точке покоящейся жидкости равно внешнему давлению, сложенному с весом столба жидкости высотой от по­верхности до данной точки и с площадью основания, равной единице.

Заметим, что закон в такой редакции верен как для несжимае­мой, так и для сжимаемой жидкостей, т.е. для всех жидкостей и газов и их смесей. ^:

Размерность всех слагаемых в уравнении (2.9) будет иметь размерность давления — Н/м².

Закономерности, определяемые уравнением (2.9), широко ис­пользуются в различных гидростатических машинах и приборах.

К таким машинам можно отнести гидравлический пресс, гидравли­ческий аккумулятор, различные системы объемных передач и пр.

Большая часть гидростатических машин и приборов исполь­зует свойства сообщающихся сосудов. Общее свойство сообща­ющихся сосудов заключается в том, что если на свободных поверх­ностях сообщающихся сосудов давление одинаково и они запол­нены одинаковой жидкостью, то во всех сосудах уровни будут одинаковыми.

Можно показать, что в сообщающихся сосудах, заполненных жидкостями с различными удельными весами, высота столбов жидкостей над уровнем раздела обратно пропорциональна удель­ным весам. Из рис. 2.3 видно, что давления в обоих сообщающихся сосудах будут одинаковы на плоскости, проведенной через по­верхность раздела 00.

Приравняв давление в этом сечении в пра­вом и левом сосудах

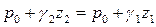получим, что .

Задача.В U образную трубу (рис. 2.4.) налиты вода и бензин. Определить плотность бензина, если Н_б=500мм, h_в=350мм. Капиллярный эффект не учитывать.

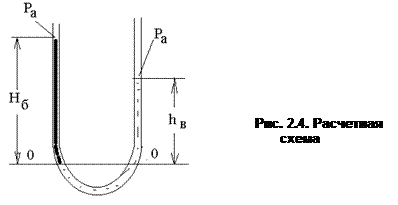По основному уравнению гидростатики – давление по сечению 0-0 одинаково как для левой, так и для правой трубы.

р_а +r_бgH_б = r_вgh_в+p_a

где p_а – атмосферное давление, для левой и правой труб одинаково;

r_в =1000кг/м³ - плотность воды.

Отсюда

r_бgH_б = r_вgh_в