
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Негравитационных массовых сил
До сих пор мы рассматривали равновесие жидкостей и газов при наличии лишь гравитационных массовых сил — сил
тяжести.
В практике имеет место равновесие жидкостей и газов при наличии негравитационных массовых сил — сил инерции и электромагнитных сил, действующих на проводящие среды. Общеё условие возможности существования равновесия, заключается в том, что массовые силы должны иметь потенциал, относится и ко всем негравитационным массовым силам.
В этом параграфе остановимся на двух случаях равновесия при наличии сил инерции.
Пример. Пусть сосуд, наполненный жидкостью, движется равноускоренно (или равнозамедленно) в горизонтальном направлении (рис. 2.5).
Из теоретической механики известно, что задачу динамики можно рассматривать как задачу статики, если к внешним силам прибавить силы инерции.
 Если сосуд движется равноускоренно с ускорением а, то при выбранной системе координат проекции напряжений массовых сил будут
Если сосуд движется равноускоренно с ускорением а, то при выбранной системе координат проекции напряжений массовых сил будут
X = a; Y = 0; Z = g.
Уравнение (2.5) после интегрирования примет вид

Произвольная постоянная С определится из условия, что при х=x0 и z = z0 давление будет р= ро, т. е.
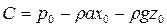 ,
,
следовательно, давление в любой точке жидкости определится по формуле

а уравнение поверхностей уровня (р =const) будет иметь вид  .
.
Если равноускоренное движение с ускорением а направлено
вертикально вниз, то массовые силы, отнесенные к единице массы, будут
 и
и 
интеграл уравнения (2.5) будет равен
 .
.
Постоянная определится из условия, что при z = z0 р = ро
т.е.
 ,
,
тогда давление в любой точке жидкости равно
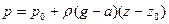 . (2.15)
. (2.15)
Уравнение поверхностей уровня будет z = const.
Из сравнения соотношения (2.15) с формулой (2.9) видим, что при таком движении уменьшается суммарное ускорение, а при а = g жидкость будет невесомой.
Очевидно, что, изменив направление движения на обратное, при том же ускорении получим эффект обратный, как бы утяжеление жидкости. Это явление наблюдается при взлете ракеты.
Задание 1. У тягача - автомобиля в течение времени t равномерно изменяется скорость от V1 до V2 , в результате чего изменяется форма свободной поверхности жидкости, которой наполнена прицепленная к нему цистерна (рис. 2.6). Диаметр цистерны D, длина L. Плотность жидкости r.
Задание:
- Вывести уравнение свободной поверхности жидкости.
- Определить, на какую высоту повысится или понизится уровень жидкости у передней стенки цистерны (по ходу автомобиля – тягача).
- Построить линию свободной поверхности жидкости.
- Определить величину избыточного гидростатического давления в точке, обозначение которой указано в исходных данных.
| Исходные данные | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| V1,км/ч | 5 | 20 | 40 | 45 | 50 | 70 | 20 | 10 | 5 |
| V2, км/ч | 20 | 5 | 30 | 25 | 35 | 39 | 10 | 30 | 25 |
| t, с | 7 | 6 | 4 | 5 | 6 | 4 | 5.5 | 6 | 5 |
| L, м | 8.7 | 14.7 | 9.4 | 10 | 9,6 | 6,7 | 12 | 14 | 12 |
| D, м | 2,2 | 3 | 2 | 2,8 | 3 | 2,6 | 2,2 | 3 | 2 |
| r, кг/м3 | 890 | 900 | 950 | 830 | 800 | 900 | 830 | 790 | 850 |
| Точка | A | B | C | A | B | C | B | A | C |
Примечание:
1. Для вывода уравнения свободной поверхности жидкости необходимо воспользоваться уравнением равновесия жидкости в дифференциальной форме.
2.
 |
Горизонтальное ускорение а, м/с2, определяется по формуле
 .
.
Дата добавления: 2015-04-18; просмотров: 267; Мы поможем в написании вашей работы!; Нарушение авторских прав |