Основное уравнение гидростатики. Для вывода основного уравнения гидростатики, уста­навливающего зависимость давления р в точке от характера дей­ствующих в жидкости массовых сил

Для вывода основного уравнения гидростатики, уста­навливающего зависимость давления р в точке от характера дей­ствующих в жидкости массовых сил, рассмотрим равновесие эле­ментарного прямоугольного параллелепипеда со сторонами dx, dy, dz, выделенного внутри покоящейся жидкости (рис. 2.2). Пусть на единицу массы параллелепипеда действует массовая сила её составляющими X, Y и Z. Если на три грани, пересе­кающиеся в точке О, будет действовать давление р, то на соот­ветствующих противоположных гранях (рис. 2.2) давления будут равны:

; .

Тогда уравнения равновесия в проекциях на оси х, y, z будут иметь вид

,

или

Три последних уравнения являются основными уравнениями гидростатикии называются уравнениями Эйлера равновесия жидкости или газа.

Эта система уравнений иногда записывается в виде:

(2.2)

Так как

,

и

,

то, очевидно, система уравнений (2.2) может быть представлена в векторном виде

(2.3)

Если систему (2.2) умножим последовательно на dx, dy, dz и сложим, то получим

Так как правая часть последнего уравнения есть полный дифференциал

, (2.4)

то уравнение (2.4) будет иметь вид

. (2.5)

Следовательно, при наличии равновесия полным дифферен­циалом должна быть и левая часть уравнения (2.4). В частности, при постоянной плотности (r = const) получим

Из этого уравнения видно, что массовые силы имеют потен­циал и проекции массовых сил можно выразить в виде:

(2.6)

Тогда уравнение (2.5) запишется таким образом:

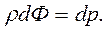
Из этого следует, то жидкость может находиться в равно­весии только в том случае, когда массовые силы, действующие в ней, имеют потенциал, т. е. проекции массовых сил удовлетво­ряют условию (2.6).

Поверхность, в каждой точке которой давление постоянно, называют поверхностью уровня. Если в уравнении (2.5) положить р = const, то уравнение поверхности уровня будет

Х dx + У dy + Z dz = О,

или

dФ = 0.

Из последнего уравнения следует, что поверхность уровня одновременно является поверхностью равного потенциала или так называемой эквипотенциальной поверхностью.