Определение координат центра давления на плоскую поверхность произвольной формы

Точка приложения силы гидростатического давления называется центром давления.рассмотрим открытый сосуд с наклонной стенкой, заполненный жидкостью. Также наметим на стенке плоскую фигуру произвольной формы и изобразим её проекцию (воспроизведём рис. 5.1. с некоторыми уточнениями в области центра давления) (рис.6.1)., сила гидростатического давления P на фигуру ω направлена по нормали к её плоскости.Эта сила P является геометрической суммой сил поверхностного PA и весового Pвес. давления.

Центр давления силы PA будет совпадать с центром тяжести, так как поверхностное давление p0 (часто p0=pатм.), передаваясь через жидкость распределяется равномерно по рассматриваемой площади ω (p0 не изменяется с глубиной в соответствии с законом Паскаля).

Центр давления Dвес. силы весового давления Pвес. будет расположен ниже центра тяжести, так как весовое давление распределено статически (в соответствии с основным уравнением гидростатики) и, значит, неравномерно по площади фигуры. Чем глубже располагается точка фигуры, тем большее давление она испытывает.Центр давления D силы абсолютного давления P найдётся в результате геометрического сложения сил PA и Pвес.

Таким образом, для определения координат точки D необходимо найти координаты точки Dвес.Найдём расстояние lD вес. (см. рис. 6.1.). Для этого будем использовать теорему Вариньона: Момент равнодействующей силы равен сумме моментов составляющих сил. (При этом далее будем рассматривать только силы весового давления.)

Рис. 6.1 К определению координат центра давления.

Запишем теорему Вариньона относительно оси OX.

- Момент равнодействующей силы весового давления:

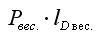
- Сумма моментов составляющих сил – частей силы Рвес., приходящихся на элементарные площадки dω. (Площадка dω определятся также, как и при выводе формулы для определения величины силы Р в п.6).

Итак, момент элементарной силы давления: , сумма моментов: 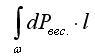Заметим, что здесь рассматриваются только силы весового давления, но не учитывается сила поверхностного давления.

Итак, теорема Вариньона:

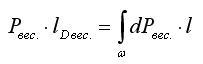
так как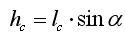

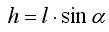
Выражение представляет собой момент инерции относительно оси OX, тогда:

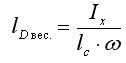Момент инерции Ix можно определить, зная величину Io момента инерции площади фигуры относительно оси, проходящей через её центр тяжести по следующей зависимости:

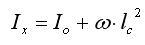
С учётом этого расстояние от оси ОХ до центра весового даления:

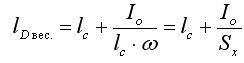(Sx – статический момент относительно оси ОХ).или

где e – эксцентриситет давления – расстояние между центром тяжести и центром избыточного давления.Для нахождения координаты ХD вес. аналогично составляют уравнение моментов относительно оси ОZ. В случае симметричной фигуры относительно вертикальной оси, проведённой через центр тяжести (точнее говоря, оси, образованной пересечением вертикальной плоскости, проведённой через центр тяжести и плоскостью фигуры) центр давления Dвес. будет располагаться на этой оси.