
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Геометрический, физический (энергетический) смысл уравнения
Бернулли. Все члены уравнения Бернулли (z+P\γ+v^2/2g=const) имеют линейную размерность, и каждый из них может называться высотой, например: z – геометрическая высота, v^2\2g– высота скоростного напора. Сформулируем геометрический смысл уравнения Бернулли. При установившемся движении жидкости элементарной струйки сумма трех высот есть величина постоянная вдоль элементарной струйки. Уравнение Бернулли (Э =zg+P/ρ+v^2/2=const)выражает один из случаев закона сохранения энергии в любом сечении элементарной струйки.
В данном уравнении каждое слагаемое представляет собой величину удельной (по отношению к массе) энергии: zg – удельная постоянная энергия положения; P/ρ – удельная потенциальная энергия давления; v^2/2= – удельная кинетическая энергия. Таким образом, энергетический смысл уравнения Бернулли заключается в следующем: при установившемся движении жидкости элементарной струйки сумма трех удельных энергий (энергии положения, энергии давления и кинетической энергии) остается неизменной вдоль элементарной струйки. В уравнении Бернулли (2.66) можно слагаемые рассматривать как удельные энергии, но уже по отношению к единице веса жидкости.
12. Уравнение Бернулли для элем.струйки реальной жидкости выражает закон сохранения энергии, связывающий удельную по весу энергию жидкости в двух сечениях потока.
При движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате, полная удельная энергия жидкости в предыдущем сечении будет больше полной удельной энергии; жидкости в последующем сечении на величину потерянной энергии. Потерянная энергия, или потерянный напор, обозначается kw и имеет линейную размерность.
Ураевнение Бернулли для реальной жидкости будет иметь вид:
z1 + p1/ρg + v1^2/2g = z2 + p2/ρg + v2^2/2g + hw
Для элементарной струйки:
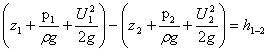
Для потока реальной жидкости
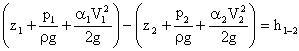
Здесь:
z1, z2 - расстояния от произвольно выбранной горизонтальной плоскости до центров тяжести рассматриваемых сечений 1,2,
p1,p2 - давления в центрах сечений,
U1,U2- местные скорости жидкости в сечениях 1 и 2,
V1,V2- средние скорости жидкости в сечениях 1 и 2,
ρ- плотность жидкости, g-ускорение силы тяжести,
h1-2 -энергия единицы веса жидкости, потраченная на преодоление сил трения между сечениями 1 и 2.
α - коэффициент Кориолиса (его значение зависит от степени неравномерности распределения скоростей в живом сечении потока, меняясь в пределах от 1 до 2).
Если ввести обозначения:
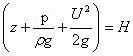
то H - полный напор, и уравнение Бернулли запишется
H1 = H2 + h1-2
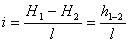 Потери напора, отнесенные к единице длины струйки, называются гидравлическим уклоном, и обычно обозначаются буквой i; таким образом
Потери напора, отнесенные к единице длины струйки, называются гидравлическим уклоном, и обычно обозначаются буквой i; таким образом
H1 — напор потока жидкости в начале участка русла;
H2 — напор потока жидкости в конце участка русла;
, где l-расстояние между сечениями, измеряемое вдоль оси струйки.
Разность 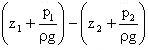 , отнесенная к единице длины струйки, называется пьезометрическим уклоном j.
, отнесенная к единице длины струйки, называется пьезометрическим уклоном j.
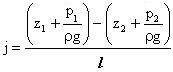
13 Водомер Вентури служит для определения расхода жидкости в напорном трубопроводе.Конструктивно он представляет собой круглую трубу переменного сечения с плавным переходом диаметров. Действие прибора основано на зависимости перепада давления между широким и узким сечениями от проходящего через них расхода жидкости. Эта зависимость может быть установлена на основании уравнения Бернулли/ Таким образом, уравнение Бернулли показывает, что, если скорость жидкости увеличивается в связи с уменьшением сечения, то давление в потоке должно понизиться. Этот принцип и используется в водомере Вентури.
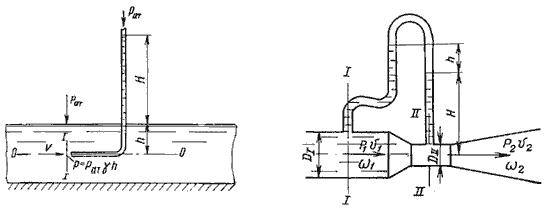
Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:
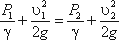
или
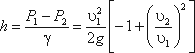
Используя уравнение неразрывности
Q = υ1ω1 = υ2ω2
сделаем замену в получено выражении:
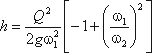
Решая относительно Q, получим
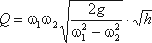
Выражение, стоящее перед 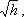 , является постоянной величиной, носящей названиепостоянной водомера Вентури.
, является постоянной величиной, носящей названиепостоянной водомера Вентури.
Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.
Дата добавления: 2015-04-18; просмотров: 362; Мы поможем в написании вашей работы!; Нарушение авторских прав |