Гидросатическое давление на криволинейную поверхность произвольной формы

(Если криволинейная поверхность не цилиндрическая Рy определяется как Рх).

8)Условие равновесия плавающих тел. Центр тяжести и центр водоизмещения. Плавучесть и остойчивость плавающих тел.

Условие равновесия плавающих тел – Закон Архимеда. На тело погруженное в жидкость действует выталкивающая сила = весу жидкости в объеме вытесненным телом. Если вес тела = подъемной силе , то тело плавает.

С – центра тяжести (всего тела)

P – центр водоизмещения (центр тяжести погруженной части тела)

Плавучесть — свойство погружённого в жидкость тела оставаться в равновесии, не выходя из воды и не погружаясь дальше, то есть плавать

Остойчивость судна – способность судна, выведенного из состояния равновесия под действием внешних сил возвращаться в состояние равновесия.

Основные понятия о движении жидкости

Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы - круг (рис.3.1, б); живое сечение клапана - кольцо с изменяющимся внутренним диаметром (рис.3.1, б).

Рис. 3.1. Живые сечения: а - трубы, б – клапана

Смоченный периметр χ ("хи") - часть периметра живого сечения, ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией).

Рис. 3.2. Смоченный периметр

Для круглой трубы

если угол в радианах, или

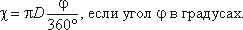
Расход потока Q - объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Гидравлический радиус потока R - отношение живого сечения к смоченному периметру

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

υ = f(x, y, z) P = φ f(x, y, z)

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

υ = f1(x, y, z, t)P = φ f1(x, y, z, t)

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока - трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Рис. 3.3. Линия тока и струйка

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное - течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

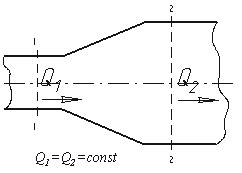Рис. 3.4. Труба с переменным диаметром при постоянном расходе

Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q1=Q2= const, откуда ω1υ1 = ω2υ2

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид: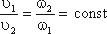

10. В гидромеханике существуют два метода изучения движения жидкости: метод Лагранжа и метод Эйлера.

1. Метод Лагранжа заключается в изучении движения каждой отдельной частицы жидкости. В этом случае движение определяется положением частицы жидкости в функции от времени t. Движение частицы будет определено, если точно определить координаты x, y, и z в заданный момент времени t, что дает возможность построить траекторию движения частицы жидкости. Величины x, y, и z являются переменными Лагранжа, а их изменения за время dt позволяет получить значение dx, dy и dz, а затем путь Проекции скорости на координатные оси определяются зависимостями , , , а местная скорость

Метод Лагранжа сводится к определению семейства траекторий движения частиц движущейся жидкости.

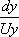
Это выражение называется уравнением линии тока. Метод Лагранжа в гидравлике не нашел широкого применения ввиду его относительной сложности.

2. Метод Эйлера основан на изучении поля скоростей, под которым понимается значение величины и скоростей во всех точках пространства, занятого движущейся жидкостью.