
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Истечение через насадки. Коэффициент расхода.
Вопрос 25. Истечение через короткие трубы в атмосферу и под уровень.
1. Под уровень
Рассматриваем Установившееся движение: скорость V в трубопроводе не изменяется во времени. Разность z уровней в сосудах А и В, соединяемых трубопроводом, постоянна(считаем, что в сосуд А жидкость всё время каким-либо образом доливается, а из сосуда В – удаляется).
Найдём велечину расхода Q для трубопровода. С это целью используем уравнение Бернули.
А) намечаем живые сечения 1-1 и 2-2. Для этих сечений известно давление р-р0 и скорости Va=Vb=0
Б) намечаем плоскость сравнения ОО. Эту плоскость удобно провести по сечению 2-2. При этом Z2 обратить в 0.
В) пишем уравнение Бернули
(1) 
Г) выясняем значения отдельных членов, входящих в это уравнение.
(2) Z1=z. V1=Va=0. V2=Vb=0. P1=P2=Pa. Z2=0. Α=1.
Z-разность уровней жидкости в сосудах А и В.
Д) подставляем 2 в 1. Получаем Z=Hf.
Как видно, при истечении под уровень разность уровней Z целиком расходуется на потери напора в трубе.
Hf=ζf*V2/2g
Ζf- полный коэффициент сопротивления для трубы.
Q=ώV=πD2/4*1/ 
2. В атмосфру
Здесь также рассматриваем установившиеся движение. V=const, H=const, Н-превышение уровня жидкости в сосуде А над центром выходного сечения.
Используя Бернули, сечения 1-1, 2-2 и плоскость сравнения ОО намечаем, как показано на чертеже. Имеем
 , V1=Va=0, V2=V, P1=P2=Pa, α=1.
, V1=Va=0, V2=V, P1=P2=Pa, α=1.
H=Hf+  /2g.
/2g.
При истечении в атмосферу напор Н тратится на потери в трубе и на образование скоростного напора в выходном живом сечении.
Получим 
28. Всасывающей трубой насоса называется туба, по которой насос засасывает жидкость из бассейна. Эта труба обычно так же как и сифон, характеризуется наличием вакуума. Найбольшая велечина вакуума будет непосредстенно у насоса, перед его рабочим колесом. Такой вакуум можно найти, соединяя уравнением Бернули сечение 1-1, намеченное по поверхности жидкости в бассейне, и сечение 2-2.

Вакуум должен удовлетворять условию (hвак)нас меньше либо равно пределу от 4,0 до 6,5 м вод. Ст.
Зная допустимый вакуум для данного насоса и данной жидкости можно найти предельное максимальное возвышение насоса над горизотом жидкости в басейне.

29. Расчёты тупиковых сетей. Тупиковых, кольцевых.
А) Тупиковых. Общий ход решения задачи. 1 Устанавливаем расчётные расходы для отдельных участков сети. Расчётный расход какого-либо участка должен равняться сумме расходов, забираемых из сети ниже(по течению) этого участка.
Q3-4=Q4. Q1-2=q4+q5+q6+q’l2-5. Q2-5=q5+0.55q’l2-5.
2 Выбираем линию трубопроводов, которую следует рассматривать как магистральную. В качестве магистрали намечаем линию: найболее нагруженную расходами, найболее длинную, характеризуемую найбольшими отметками дельта поверхности земли. Если магистраль будет намечена неудач но, то в конце расчёта получим некоторую неувязку, причём расчёт придётся выполнять заново, задавшись новым направлением магистрали.
Б) Кольцевых. Задаёмся диаметрами отдельных труб, направлением движения воды в трубе 4-5,(слева на право), распределением расхода q5 между линиями 4-5 и 6-5, здесь считаем что расход линии равен 4-5 равен ξq5, а расход линии 6-5 равен (1-ξ)q5,причём задаёмся величиной ξ.
В рассматриваемом кольце труб имеются два разных потока: один против часов, другой по. Задавшись направлением воды, мы назначим встречу потоков в точке 5. Она называется нулевой.
30. Расчёт разветвлённой тупиковой сети водопровода.
Построив пьзометрическую линию для магистрали, мы тем самым задали напоры в начале каждого ответвления. В связи с этим: а) опредиляем потерю напора в ответвлении  где дельта 3 известна из расчёта магистрали. Б) переписываем формулу
где дельта 3 известна из расчёта магистрали. Б) переписываем формулу 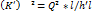 в) по соответствующим таблицам, зная К’, находим диаметр D’. Полученное значение D’ округляем до ближайшего большего сортаментного значения. Г) По найденому Д опредиляем модуль К и вычисляем действительные потери.
в) по соответствующим таблицам, зная К’, находим диаметр D’. Полученное значение D’ округляем до ближайшего большего сортаментного значения. Г) По найденому Д опредиляем модуль К и вычисляем действительные потери.
26. Гидравлический расчёт длинных трубопроводов 
27. Формулы для гидравлического расчёта коротких трубопроводов 

31.Вакуумметрическая высота или высота вакуума – высота столба жидкости
(заданного удельного веса), уравновешивающего разность атмосферного и абсолютного
гидромеханического давлений в рассматриваемой точке.
Важным гидравлическим параметром насоса является допустимая вакууметрическая высота всасывания, характеризующая нормальные условия подхода жидкости к рабочему колесу. Эта величина выражается в метрах водяного столба при температуре 20°С и при нормальном атмосферном давлении (10 м водяного столба). В силу разных причин, в том числе из-за сложности физического процесса, происходящего на всасывании насоса, этому важнейшему параметру при эксплуатации и при подборе насосов не уделяется должного внимания.
32. Параллельным соединением называют такую коммутацию, при которой несколько насосов осуществляют подачу в один общий напорный коллектор или нагнетательный трубопровод. При подборе насосов для параллельной работы следует учитывать множество факторов, наиглавнейшим из которых является т.н. равенство напоров.
Последовательным называют такое соединение, при котором жидкость, получившая энергию от насоса, подается во всасывающий патрубок следующего агрегата. В таких случаях увеличение напора происходит ступенчато, от насоса к насосу. Поэтому насосы, соединенные по такому принципу, делят на агрегаты первой, второй, и т.д. ступеней. При последовательном подключении насосов необходимо учитывать прочность корпуса агрегатов второго и последующих уровней, т.к. не все насосы в состоянии выдерживать избыточное давление в течение длительного времени.
33. Совместная работа насоса и трубопровода.
Необходимость совместного включения насосов возникает в случаях, когда один насос не может обеспечить необходимую подачу или напор, либо необходим резерв для обеспечения бесперебойности подачи воды.
Для увеличения подачи используется параллельное соединение насосов, когда два (или более) насосов подают воду в один трубопровод. Для определения параметров работы насоса в этом случае строится совместная характеристика этих насосов. Она образуется суммированием производительности насосов при различных напорах
34. Гидравлический удар (явление гидравлического удара) – повышение или понижение гидромеханического давления, в напорном трубопроводе вызванное изменением во времени в каком-либо сечении трубопровода скорости движения жидкости (например, путем открытия или закрытия задвижки). Увеличение давления при Г. у. определяется в соответствии с теорией Н. Е. Жуковского по ф-ле:
Dр=r(v0-v1)c,
где Ар — увеличение давления в Па, r — плотность жидкости в кг/м3, v0 и v1 — ср. скорости в трубопроводе до и после закрытия задвижки в м/с, с — скорость распространения ударной волны вдоль трубопровода.
35.Гидравлический удар прямой (или начальный) – волна положительного или
отрицательного гидравлического удара, распространяющаяся вдоль напорного трубопровода от
места возникновения гидравлического удара до места, где он отражается
Гидравлический удар отраженный (непрямой) – волна положительного или
отрицательного гидравлического удара, возникшая благодаря отражению от какого-либо 3
«препятствия» или водоема гидравлического удара, подошедшего к этому «препятствию» или
Водоему
Гидравлический удар полный – наибольшая величина постепенно нарастающего (до
определенной величины) гидравлического удара не сниженная отраженным ударом (имеющим
другой знак и не успевшие дойти к месту зарождения данного прямого гидравлического удара
до момента завершения его роста).
Гидравлический удар неполный – наибольшая величина гидравлического удара,
получающаяся в месте зарождения прямого гидравлического удара, при условии, что
отраженный удар успевает придти к указанному месту раньше, чем постепенно нарастающий
прямой гидравлический удар достигнет полной своей величины
36.Безнапорный поток- поток, имеющий место при безнапорном движении – движется без напора, то есть под действием собственного веса, не заполняя весь объём трубы, тунеля.
Формула Шези — формула для определения средней скорости потока при установившемся равномерном турбулентном движении жидкости в области квадратичного сопротивления для случая безнапорного потока. Применяется для расчётов потоков в речных руслах и канализационых системах.
 ,
,
де V — средняя скорость потока, м/с;
C — коэффициент сопротивления трения по длине (коэффициент Шези), являющийся интегральной характеристикой сил сопротивления;
R — гидравлический радиус, м;
I — гидравлический уклон м/м.
Коэффициент Шези можно определить по формуле Маннинга
 ,
,
где n — коэффициент шероховатости стенок трубы или канала;
R — гидравлический радиус, подставляемый вметрах.
Коэффициент п принимают в зависимости от материала труб.
Коэффициент шероховатости – определяемое на основании опытов именованное
(размерное) число, характеризующее степень шероховатости стенок русла (величину выступов
шероховатости, их форму и т. п.)
Таким образом, приведённые формулы позволяют осуществлять гидравлический расчёт любых безнапорных потоков. Обычно для расчётов используются вспомогательные таблицы или номограммы, составленные на основе формулы Шези.
Отметим, что формула Шези справедлива для потоков с турбулентным режимом. Таких потоков на практике подавляющее большинство.
37.Движение воды в русле канала. Открытые русла могут быть естественными или искусственными. К естественным открытым руслам относятся реки и ручьи, к искусственным– каналы, безнапорные трубы (например, дренажные),гидротехнические тунели и т. д. Особенность движения в открытом русле заключается в том, что поток здесь ограничен не со всех сторон, а имеет свободную поверхность, все точки которой находятся под воздействием одинакового внешнего давления (атмосферного)
Нормальной называется глубина, которая установилась бы в данном русле, если движение в русле равномерное.
38,Удельную энергию в данном живом сечении, определенную относительно горизонтальной плоскости, проходящей через низшую точку этого сечения, будем называть удельной энергией сечения и обозначать символом Э. Удельной энергией сечения называется частное значение полной удельной энергии, когда плоскость сравнения проведена через самую низшую точку сечения потока.
 На рис. 4.4 показан график зависимости удельной энергии сечения от глубины. Глубина hк, при которой удельная энергия сечения минимальна, называется критической.
На рис. 4.4 показан график зависимости удельной энергии сечения от глубины. Глубина hк, при которой удельная энергия сечения минимальна, называется критической.
39,Потоки, имеющие глубину ниже критической, называются бурными, потоки с глубиной выше критической – спокойными. Если глубина потока равна критической, то такое состояние потока называется критическим. Число́ Фру́да (  ), или критерий Фруда, — один из критериев подобия движения жидкостей и газов, является безразмерной величиной. Применяется в случаях, когда существенно воздействие внешних сил Число Фруда характеризует соотношение между силой инерции и внешней силой, в поле которой происходит движение, действующими на элементарный объём жидкости или газа:
), или критерий Фруда, — один из критериев подобия движения жидкостей и газов, является безразмерной величиной. Применяется в случаях, когда существенно воздействие внешних сил Число Фруда характеризует соотношение между силой инерции и внешней силой, в поле которой происходит движение, действующими на элементарный объём жидкости или газа:

где  — характерный масштаб скорости,
— характерный масштаб скорости,  — ускорение, характеризующее действие внешней силы ,
— ускорение, характеризующее действие внешней силы , 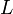 — характерный размер области, в которой рассматривается течение.
— характерный размер области, в которой рассматривается течение.
При переходе потока из спокойного состояния в бурное происходит явление гидравлического водопада, а при переходе из бурного состояния в спокойное - явление гидравлического прыжка.
Дата добавления: 2015-04-18; просмотров: 330; Мы поможем в написании вашей работы!; Нарушение авторских прав |