Метод средних величин.

Роль средних величин заключается в обобщении, т. е. замене множества индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Средняя величина обобщает качественно однородные значения признака и, следовательно, является типической характеристикой признака в данной совокупности.

Средняя арифметическая – это среднее слагаемое, при расчете которого общий объем признака в совокупности распределяется поровну между всеми единицами. Например, средняя зарплата – это такая величина заработной платы, которая приходилась бы на одного работника, если бы фонд заработной платы распределялся между всеми сотрудниками поровну.

Если объем совокупности велик и представляет собой ряд распределения, используют значение средневзвешенной арифметической средней:

.

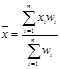Помимо средней арифметической используются и другие формы средних величин. В первую очередь это средняя геометрическая, которая позволяет сохранить неизменным на сумму, а произведение индивидуальных значений величины

.

Основное применение средняя геометрическая находит при изучении темпов роста.

Еще один показатель, характеризующий средние величины – средняя гармоническая. Он используется в случаях, когда необходимо, чтобы при усреднении оставалась неизменной сумма величин, обратных индивидуальным значениям признака. Формула расчета средней гармонической:

.

В финансовом анализе широко используется также средняя хронологическая. Для анализа предприятия применяются интервальные и моментные показатели. Первые – товарооборот, прибыль, объем поступлений, вторые – данные о запасах, основных средствах, баланс. Для усреднения моментных показателей применяется формула средней хронологической.

.