Методы многопараметрического анализа. Задача кластерного анализа. Методы древовидной кластеризации. Форма представления результатов.

Основные понятия математической статистики. Теоретические и эмпирические оценки начальных и центральных моментов.

Основные понятия математической статистики. Теоретические и эмпирические оценки ковариационных и корреляционных моментов.

Особую роль играет второй смещенный центральный момент:

,

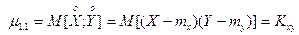называемый корреляционным моментом (иначе - "моментом связи")случайных величин Х и Y.

Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо рассеивания величин Х и Y, еще и связь между ними. Для того, чтобы убедиться в этом отметим, что корреляционный момент независимых случайных величин равен нулю.

Заметим, что корреляционный момент характеризует не только зависимость величин, но и их рассеивание. Поэтому для характеристики связи между величинами (Х;Y) в чистом виде переходят от момента K_xy к характеристике

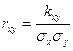
, (3)

где σ_x, σ_y - средние квадратичные отклонения величин Х и Y. Эта характеристика называется коэффициентом корреляции величин Х и Y.

Основные понятия математической статистики. Теоретические и эмпирические оценки автокорреляции, автокорреляционное расстояние.

Автокорреляция - корреляция ряда X с самим собой, с задержкой на k наблюдений.

Пусть X(t) - значение случайного процесса в момент времени t. Если X(t) имеет среднее значение m и дисперсию D, то вычисление коэффициентов автокорреляции r(k) осуществляется следующим образом.

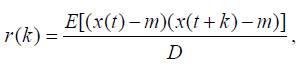
где "E" - это математическое ожидание.

Предполагая порядок процесса k-1, стандартная ошибка r(k) определяется:

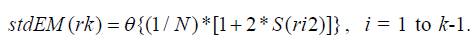N - число наблюдений ряда.

В статистике имеется несколько выборочных оценок теоретических значений автокорреляции r(k) процесса по конечному временному ряду из n наблюдений. Наиболее популярной оценкой является нециклический коэффициент автокорреляции с задержкой k:

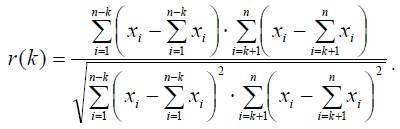
Наиболее важным из различных коэффициентов автокорреляции является первый - r1, измеряющий тесноту связи между уровнями x(1), x(2) ,..., x(n -1) и x(2), x(3), ..., x(n).

Последовательность коэффициентов корреляции rk , где k  1, 2,...,n , как функция интервала k между наблюдениями называется автокорреляционной функцией (АКФ).

Методы многопараметрического анализа. Задача кластерного анализа. Методы древовидной кластеризации. Форма представления результатов.

КА позволяет:

- Проведение классификации объектов с учетом признаков, отражающих сущность, природу объектов. Решение такой задачи, как правило, приводит к углублению знаний о совокупности классифицируемых объектов;

- Проверка выдвигаемых предположений о наличии некоторой структуры в изучаемой совокупности объектов, т.е. поиск существующей структуры;

- Построение новых классификаций для слабоизученных явлений, когда необходимо установить наличие связей внутри совокупности и попытаться привнести в нее структуру.