Методы многопараметрического анализа. Задача дискриминантного анализа (ДА). Ограничения на исходные данные. Применение функции Фишера и расстояния Махаланобиса в ДА

Дискриминантный анализ позволяет выяснить, действительно ли группы различаются между собой, и каким образом (какие переменные вносят наибольший вклад в имеющиеся различия).

Ограничения: 1- ни одна переменная не может быть линейной комбинацией других переменных. 2-закон распределения для каждой переменной имеет нормальное распределение при фиксированных значениях остальных переменных.

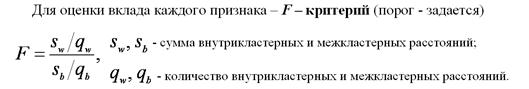
Расстояние Махаланобиса: d(Xi,Xj)=(Xi-Xj)T * S -1 *(Xi-Xj)

где xik , x jk - значения k-й переменной i-го и j-го объекта; Xi , X j - векторы значений переменных у i-го и j-го объектов; S* - общая ковариационная матрица.

линейный дискриминант Фишера

Предположим, что два наблюдаемых класса имеют средние и ковариационные матрицы .Тогда для линейной комбинации признаков средними будут , а ковариационные матрицы будут иметь вид для .Фишер взял за расстояние между этими распределениями величину, равную отношению межклассовой дисперсии к внутриклассовой:

Эта величина в некотором смысле характерезует соотношение сигнал-шум для разметки классов.Можно показать, что наилучшим образом классы разделимы при

.

Если выполняются предположения нормальности и равенства дисперсий, то полученное выше равенство эквивалентно ЛДА.

11. Методы многопараметрического анализа. Модели дискриминантного анализа (ДА): стандартная, пошаговый ДА с включением и исключением, форма представления результатов, критерий Уилкса

1- одновременное введение всех переменных, в этом случае учитывается каждая независимая переменная, при этом ее дискриминирующая сила не учитывается.

Альтернативой является пошаговый дискриминантный анализ, при котором переменные вводятся последовательно, исходя из их способности различить (дискриминировать) группы.

При пошаговом анализе «с включением» на каждом шаге просматриваются все переменные, и находится та из них, которая вносит наибольший вклад в различие между совокупностями. Эта переменная должна быть включена в модель на данном шаге, и происходит переход к следующему шагу.

При пошаговом анализе «с исключением» движутся в обратном направлении, в этом случае все переменные сначала будут включены в модель, а затем на каждом шаге будут устраняться переменные, вносящие малый вклад в различение. Тогда в качестве результата успешного анализа можно сохранить только «важные» переменные в модели, т.е. те переменные, чей вклад в дискриминацию больше остальных. Пошаговый дискриминантный анализ основан на использовании уровня значимости F-статистики.