
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы многопараметрического анализа. Задача кластерного анализа. Метод k-средних. Форма представления результатов.
Метод k-средних.Наряду с иерархическими методами классификации, рассмотренными в ранее, существует многочисленная группа так называемых итеративных методов кластерного анализа. Предположим, мы уже имеем гипотезы относительно числа кластеров (по наблюдениям или по переменным). Вы можете указать системе образовать ровно три кластера так, чтобы они были настолько различны, насколько это возможно. Это именно тот тип задач, которые решает алгоритм метода k-средних.
В общем случае метод k-средних строит ровно K различных кластеров, расположенных на возможно больших расстояниях друг от друга. Сущность их заключается в том, что процесс классификации начинается с задания некоторых начальных условий (количество образуемых кластеров, порог завершения процесса классификации и т. д.).
Итеративные методы в большей степени, чем иерархические, требуют от пользователя интуиции при выборе типа классификационных процедур и задания начальных условий разбиения, так как большинство этих методов очень чувствительны к изменению задаваемых параметров. Например, выбранное случайным образом число кластеров может не только сильно увеличить трудоемкость процесса классификации, но и привести к образованию «размытых» или мало наполняемых кластеров. Поэтому целесообразно сначала провести классификацию по одному из иерархических методов или на основании экспертных оценок, а затем уже подбирать начальное разбиение и статистический критерий для работы итерационного алгоритма.
Как и в иерархическом кластерном анализе, в итерационных методах существует проблема определения числа кластеров. В общем случае их число может быть неизвестно. Не все итеративные методы требуют первоначального задания числа кластеров. Но для окончательного решения вопроса о структуре изучаемой совокупности можно испробовать несколько алгоритмов, меняя либо число образуемых кластеров, либо установленный порог близости для объединения объектов в кластеры. Тогда появляется возможность выбрать наилучшее разбиение по задаваемому критерию качества.
В отличие от иерархических процедур метод k-средних не требует вычисления и хранения матрицы расстояний или сходств между объектами. Алгоритм этого метода предполагает использование только исходных значений переменных. Для начала процедуры классификации должны быть заданы k случайно выбранных объектов, которые будут служить эталонами, т.е. центрами кластеров. Считается, что алгоритмы эталонного типа удобные и быстродействующие. В этом случае важную роль играет выбор начальных условий, которые влияют на длительность процесса классификации и на его результаты.
С вычислительной точки зрения можно рассматривать этот метод, как дисперсионный анализ "наоборот". Программа начинает с K случайно выбранных кластеров, а затем изменяет принадлежность объектов к ним, чтобы: 1) минимизировать изменчивость внутри кластеров, и 2) - максимизировать изменчивость между кластерами.
Обычно, когда результаты кластерного анализа методом к- средних получены, можно рассчитать средние для каждого кластера по каждому измерению, чтобы оценить, насколько кластеры различаются друг от друга. В идеале вы должны получить сильно различающиеся средние для большинства, если не для всех измерений, используемых в анализе. Значения F-статистики, полученные для каждого измерения, являются другим индикатором того, насколько хорошо соответствующее измерение дискриминирует кластеры.
6. Методы многопараметрического анализа. Задача кластерного анализа. Алгоритм CLOPE: критерий разделения на кластеры, градиент, функция стоимости.


7. Методы многопараметрического анализа. Задача кластерного анализа. Алгоритм CLOPE: этапы алгоритма кластеризации, задача кластеризации по алгоритму, вычислительная сложность алгоритма.
Пусть имеется база транзакций D, состоящая из множества транзакций {t1,t2,…,tn}. Каждая транзакция есть набор объектов {i1,…,im}. Множество кластеров {C1,…,Ck} есть разбиение множества {t1,…,tn}, такое, что C1 … Ck={t1,…,tn} и Ci <> ^Сi Cj = 1<=i, j<=k. Каждый элемент Ci называется кластером, n, m, k – количество транзакций, количество объектов в базе транзакций и число кластеров соответственно.
Каждый кластер C имеет следующие характеристики:
D(C) – множество уникальных объектов; Occ(i,C) – количество вхождений (частота) объекта i в кластер C; 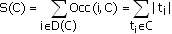 W(C) = |D(C)|; H(C) = S(C)/W(C). W(C) = |D(C)|; H(C) = S(C)/W(C).
|
Гистограммой кластера C называется графическое изображение его расчетных характеристик: по оси OX откладываются объекты кластера в порядке убывания величины Occ(i,C), а сама величина Occ(i,C) – по оси OY (рис. 2).
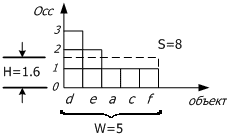
Рисунок 2. Иллюстрация гистограммы кластера
На рис. 2 S(C), равное 8, соответствует площади прямоугольника, ограниченного осями координат и пунктирной линией. Очевидно, что чем больше значение H, тем более "похожи" две транзакции. Поэтому алгоритм должен выбирать такие разбиения, которые максимизируют H.
Однако учитывать одно только значение высоты H недостаточно. Возьмем базу, состоящую из 2х транзакций: {abc, def}. Они не содержат общих объектов, но разбиение {{abc, def}} и разбиение {{abc}, {def}} характеризуются одинаковой высотой H=1. Получается, оба варианта разбиения равноценны. Но если для оценки вместо H(C) использовать градиент G(C)=H(C)/W(C)=S(C)/W(C)2, то разбиение {{abc},{def}} будет лучше (градиент каждого кластера равен 1/3 против 1/6 у разбиения {{abc, def}}).
Обобщив вышесказанное, запишем формулу для вычисления глобального критерия – функции стоимости Profit(C):
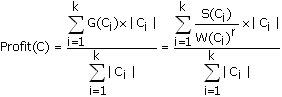
|Ci| – количество объектов в i-том кластере, k – количество кластеров, r – положительное вещественное число большее 1.
С помощью параметра r, названного авторами CLOPE коэффициентом отталкивания (repulsion), регулируется уровень сходства транзакций внутри кластера, и, как следствие, финальное количество кластеров. Этот коэффициент подбирается пользователем. Чем больше r, тем ниже уровень сходства и тем больше кластеров будет сгенерировано.
Формальная постановка задачи кластеризации алгоритмом CLOPE выглядит следующим образом: для заданных D и r найти разбиение C: Profit(C,r) -> max.
Дата добавления: 2015-04-21; просмотров: 383; Мы поможем в написании вашей работы!; Нарушение авторских прав |