Дифференцирование сложных ф.м.п. Производная по направлению.

Теорема.Пусть u = f (х, у) задана в области D и пусть х = х(t ) и у = у(t ) определены в области , причём, когда , то х и у принадлежат области D . Пусть функция u дифференцируема в точке M₀(x₀, y₀, z₀), а функции х(t ) и у(t ) дифференцируемы в соответствующей точке t₀, то сложная функция u = f [x(t), y(t)]=F (t) дифференцируема в точке t₀ и имеет место равенство:

.

Доказательство.Так как u дифференцируема по условию в точке (x₀, y₀), то её полное приращение представляется в виде

.

Разделив это соотношение на , получим:

.

Перейдём к пределу при и получим формулу

.

Замечание 1.Если u = u(x, y) и x = x, y = y(x), то полная производная функции u по переменной х

или .

Последнее равенство можно использовать для доказательства правила дифференцирования функции одной переменной, заданной неявно в виде F(x, y) = 0, где y = y(x) (см. тему № 3 и пример 14).

Имеем: . Отсюда . (6.1)

Вернёмся к примеру 14 темы № 3:

;

;

;

.

Как видим, ответы совпали.

Замечание 2. Пусть u = f (х, у), где х = х(t , v), у = у(t , v). Тогда u есть в конечном счёте сложная функция двух переменных t и v . Если теперь функция u дифференцируема в точке M₀ (x₀, y₀), а функции х и у дифференцируемы в соответствующей точке (t₀, v₀), то можно говорить о частных производных по t и v от сложной функции в точке (t₀, v₀). Но если мы говорим о частной производной по t в указанной точке, то вторая переменная v считается постоянной и равной v₀. Следовательно, речь идёт о производной только от сложной функции по t и, следовательно, мы можем воспользоваться выведенной формулой. Таким образом, получим:

и .

Пример 13.Найти полную производную функции u = x ^y,где x =sint, y =cost .

.

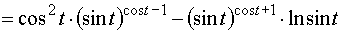Рассмотрим функцию u(x, y, z) в точке М( x, y, z) и точке М₁( x + Dx, y + Dy, z + Dz).

Проведем через точки М и М₁ вектор . Углы наклона этого вектора к направлению координатных осей х, у, z обозначим соответственно a, b, g. Косинусы этих углов называются направляющими косинусамивектора .

Расстояние между точками М и М₁ на векторе обозначим DS.

Высказанные выше предположения, проиллюстрируем на рисунке:

z

M

M₁

y

x

Далее предположим, что функция u(x, y, z) непрерывна и имеет непрерывные частные производные по переменным х, у и z. Тогда правомерно записать следующее выражение:

,

где величины e₁, e₂, e₃ – бесконечно малые при .

Из геометрических соображений очевидно:

Таким образом, приведенные выше равенства могут быть представлены следующим образом:

;

Заметим, что величина s является скалярной. Она лишь определяет направление вектора .

Из этого уравнения следует следующее определение:

Определение: Предел называется производной функции u(x, y, z) по направлению вектора в точке с координатами ( x, y, z).

Поясним значение изложенных выше равенств на примере.

Пример. Вычислить производную функции z = x² + y²x в точке А(1, 2) по направлению вектора . В (3, 0).

Решение. Прежде всего необходимо определить координаты вектора .

=(3-1; 0-2) = (2; -2) = 2 .

Далее определяем модуль этого вектора:

=

Находим частные производные функции z в общем виде:

Значения этих величин в точке А :

Для нахождения направляющих косинусов вектора производим следующие преобразования:

=

За величину принимается произвольный вектор, направленный вдоль заданного вектора, т.е. определяющего направление дифференцирования.

Отсюда получаем значения направляющих косинусов вектора :

cosa = ; cosb = -

Окончательно получаем: - значение производной заданной функции по направлению вектора .

Градиент.

Определение: Если в некоторой области D задана функция u = u(x, y, z) и некоторый вектор, проекции которого на координатные оси равны значениям функции u в соответствующей точке

,

то этот вектор называется градиентомфункции u.

При этом говорят, что в области D задано поле градиентов.

Связь градиента с производной по направлению.

Теорема: Пусть задана функция u = u(x, y, z) и поле градиентов

.

Тогда производная по направлению некоторого вектора равняется проекции вектора gradu на вектор .

Доказательство: Рассмотрим единичный вектор и некоторую функцию u = u(x, y, z) и найдем скалярное произведение векторов и gradu.

Выражение, стоящее в правой части этого равенства является производной функции u по направлению s.

Т.е. . Если угол между векторами gradu и обозначить через j, то скалярное произведение можно записать в виде произведения модулей этих векторов на косинус угла между ними. С учетом того, что вектор единичный, т.е. его модуль равен единице, можно записать:

Выражение, стоящее в правой части этого равенства и является проекцией вектора gradu на вектор .

Теорема доказана.