Основные характеристики волновых процессов. Виды волн (плоские, сферические, цилиндрические). Суперпозиция волн. Когерентность. Интерференция. Стоячие волны.

Волна – процесс распространения гармонических колебаний в упругой среде.

Источники колебания:

-точечные

-линейные

-трёхмерные

Упругая среда – её частицы связаны упругими силами (k-жётскость). Параметры упругой среды (k и m) могут быть сосредоточены в узлах (m) и междоузлах (k)

Смещение частицы в точке (1)

S₁=Acosωt₁ (t₁ – время колебаний в точке 1)

в точке (2)

S₂=Acosωt₂

t₂=t₁-x/v

S₂=Acosω(t-x/v)=Acos2π(t/T-x/λ)=Acos(ωt-k_xX)

(k_x=2π/x=ω/v – волновое число вдоль икса)

Длина волны (расстояния, пройдённое за T)

λ=v/ню

для y и z аналогичные уравнения.

k=k_xi+k_yj+k_zk, и для волны в произвольном виде имеем:

S=Acos(ωt-kr), где kr= k_xx+k_yy+k_zz (скалярное произведение)

Волновой вектор K всегда направлен перпендикулярно волновому фронту и = 2π/λ

Монохроматическая волна – волна с одной частотой, k и λ

Волновая поверхность – на ней фаза волны постоянна.

По форме волны:

1) Сферические (с точечным источником)

2) Цилиндрические (с линейным источником)

3) Плоские (от ∞-далёкого источника)

Волновой фронт – волновая поверхность, которая разделяет области, где есть колебания частиц среды и области, где их нет.

Закон движения

плоской волны

S=Acos(ωt-kr), где k – волновое число = 2π/λ

сферической волны

S=(a/r)cos(ωt-kr)

цилиндрической волны

S=(a/sqrt(r))cos(ωt-kr)

Суперпозиция – независимое сложение волн без взаимных искажений в линейной упругой среде. (Линейная среда – в ней результат действия волны (смещение частиц среды) пропорционален амплитуде волны)

Когерентность – согласованность волн по фазе (φ₁-φ₂=const)

Интерференция – суперпозиция когерентных волн, сопровождается перераспределением интенсивности волн в пространстве (сопровождается появлениям max и min интерференции)

A²=A₁²+A₂² + 2A₁A₂cos(φ₁ - φ₂)

Суммарная интенсивность

I=I₁+I₂+2sqrt(I₁I₂)cos(φ₁ - φ₂)

При суперпозиции без интерференции

I= I₁+I₂

Суперпозиция при интерференции

а) максимум интерференции

I=I₁+I₂+2sqrt(I₁I₂)

б) минимум интерференции

I=I₁+I₂ - 2sqrt(I₁I₂)

Стоячая волна

- частный случай интерференции двух одинаковых встречных волн

S₁ по ОХ, S₂ против ОХ

S₁=Acos(ωt-k_xx+φ₁), S₂=Acos(ωt+k_xx+φ₂),

S= S₁+S₂=

=2Acos(-k_xx+(φ₁-φ₂)/2)*cos(ωt+(φ₁+φ₂)/2)

S=2Acosk_xxcosωt – это не волна! а гармонические колебания с частотой ω и амплитудой А. Не переносит энергию в пространстве, как бегущая волна.

Анализ стоячей волны по х. Узлы и пучности.

а) для пучностей A(x)-2A=A_max

|x_пучн|=2πλ/4
б) для узлов A(x)=0=A_min

x_узлов=|(n+1/2)λ/2|=(2n+1)λ/4

Анализ стоячей волны по t

a) при t=0 cosωt=1

S=2Acosk_xx

Пучность на стенке получается, если стенка из более «слабого» материала, узел на стенке – если материал «сильнее»

б) t=T/4, ω=2π/T

cosωt=0

в) t=T/2

cosωt=1

Соотношения между разностью хода и Δφ

Δφ=kΔx=(2π/λ)Δx

10. Волновое уравнение. Соотношение неопределённостей для волновых процессов. Групповая и фазовая скорости волн.

Уравнение в частных производных второго порядка, линейное, однородное. Получили его с помощью закона плоской волны.

δ²S/δx²+δ²S/δy²+δ²S/δz²=(1/v²)*δ²S/δt² (v – фазовая скорость)

В результате дифференцирования закона движения:

δ²S/δx²+δ²S/δy²+δ²S/δz²= -Ak²cos(ωt-kr) k=ω²/v²

δ²S/δx²+δ²S/δy²+δ²S/δz²=(δ²/δx²+δ²/δy²+δ²/δz²)S=

=ΔS=(1/v²)*δ²S/δt² Δ= оператор Лапласа

Волновой пакет (группа волн)

Сумма монохроматических компонент:

S(x,t) =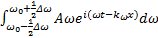

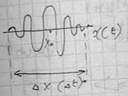
Скорость центра x_­­­₀ – групповая скорость.

ΔS=(1/v_фаз²)*δ²S/δt²

При х=х₀ – синфазность всех монохроматических составляющих пакета.

φ=ωt+k_xx (k=ω/v=2π/λ)

dφ/dk=0=(dω/dk)t-x₀

x₀=(dω/dk)t=U(t)

Соотношение неопределённостей для волновых процессов.

Для любого х волнового пакета (за исключением х₀) Δφ компонент пакета должен быть меньше π (при Δφ=π компоненты уничтожат друг друга, т.к. они противофазны)

Δφ=(dφ/dk)Δk меньше или равно π

dφ/dk=d(ωt+k_xx)/dk=(dω/dk)t-x=x₀-x

Δφ=(dφ/dk)Δk=(x₀-x)Δk меньше или равно π

при 2(x₀-x)=Δx будем иметь

ΔxΔk_x меньше или = 2π çconst (первое соотношение неопределённостей Δx и Δk_x)

Следствия:

1) В узком пакете (Δх мало) набор волновых чисел Δk большой.

2) При уменьшении Δk (возрастание монохроматичности волн пакета) Δх возрастает. при (Δk→0 Δх→∞) монохроматическая волна бесконечна в пространстве.

Аналогично получаем второе соотношение неопределённостей.

ΔωΔt меньше или = 2π

из Δφ=(dφ/dω)Δω меньше или = π

2(t-t₀)Δω меньше или = 2π

Следствие:

При возрастании монохроматичности волнового пакета (Δω→0) имеемΔt→∞ çмонохроматическая волна бесконечна во времени

Соотношение групповой (U) и фазовой (v_фаз) скоростей.

U=dω/dk=d(2πню)/d(2π/λ)= -λ²⁽dню/dλ)

v/λ=ню=λ²((1/λ²)v_φ-(1/λ)(dv_φ/dλ))

U=v₀-λ(dv_φ/dλ)

таким образом, U>v_φ при (dv_φ/dλ)<0 и наоборот (dv_φ/dλ – дисперсия (зависимость фазовой скорости волн от частоты или длины волны)).