Теорема об углах, вписанных в окружность.

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

[П] Угол, вписанный в окружность, равен половине соответствующего центрального угла.

Дано: ABC — вписанный, О — центр окружности.





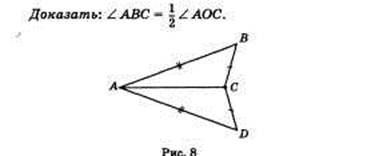
Доказательство. Рассмотрим сначала частный случай, когда одна из сторон угла проходит через центр окружности (рис. 9, а).

Треугольник АОВ равнобедренный, так как у него стороны ОА и ОВ равны как радиусы. Поэтому углы А и В треугольника равны. А так как их сумма равна внешнему углу треугольника при вершине О, то угол В треугольника равен половине угла АОС, что и требовалось доказать.

Общий случай сводится к рассмотренному частному случаю проведением вспомогательного диаметра BD (рис. 9, б, в).

В случае, представленном на рисунке 9, б,



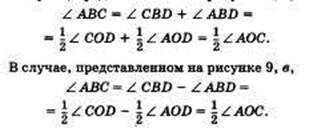
[А] Вписанный угол измеряется половиной дуги, на которую он опирается.

Дано: ABC — вписанный, О — центр окружности, АС соответствует ABC (рис. 10).

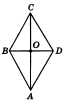
10. Задача по теме «Площадь».

Найдите площадь ромба, если его диагонали равны 6 см и 8 см.

Решение. Диагонали ромба взаимно перпендикулярны, поэтому они делят ромб на четыре равных прямоугольных треугольника. Так как диагонали ромба точкой пересечения делятся пополам, то катеты каждого из этих треугольников равны 3 см и 4 см;

11. Задача по теме «Трапеция».