Вопрос № 4. Фазовые равновесия в двухкомпонентных системах. Диаграммы плавкости. Правило рычага.

Двухкомпонентные системы могут быть представлены механическими смесями и растворами. Поскольку в механических смесях вещества ведут себя независимо друг от друга, то диаграммы состояния для механических смесей не строят. Для растворов диаграммы состояния отражают зависимость тех или иных свойств раствора от состава и температуры. Частный случай таких диаграмм (диаграммы плавкости) используется для оценки фазовых равновесий при разных температурах для разных по составу растворов. На этих диаграммах наносятся характерные температурные точки, которые отвечают началу или завершению процессов затвердевания в случае понижения температуры или, наоборот, появления новых порций жидкости и полному расплавлению – в случае повышения температуры.

Рассмотрим диаграмму плавкости двухкомпонентной системы с простой эвтектикой.

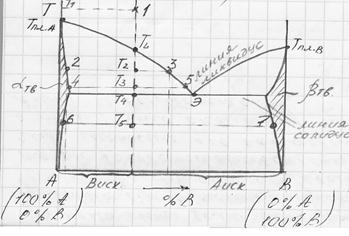Вещества в твердом виде могут образовывать ограниченные твердые растворы: 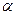- на основе вещества

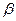-на основе вещества

Предел растворимости вещества А в 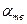показан в виде кривых справа от области раствора; предел растворимости вещества В в 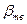– это кривые слева от заштрихованной области.

Линия ликвидус – это совокупность температурных точек, выше которых система становится жидкостью .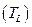

Линия солидус – это совокупность температурных точек, ниже которых система полностью затвердевает, или выше которых появляются первые порции жидкости .

Таким образом, из диаграммы видно, что все сложные системы плавятся или затвердевают не при определенной температуре, как чистые вещества, а в интервале температур, протяженность которого зависит от состава системы.

На диаграмме а точке 1 имеем однородную жидкость определенного состава. При охлаждении в интервале температур от 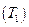до 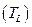никаких фазовых превращений не происходит, понижается только температура жидкости, естественно, что меняются физико-химические свойства жидкости и ее компонентов. При температуре 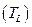наступает насыщение исходного раствора и из него появляется новая фаза. В данном случае, это кристаллы твердого раствора. Чтобы новая фаза была устойчивой, необходимо некоторое переохлаждение (ниже 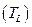), тогда зародыши новой фазы становится устойчивыми, а жидкость, в которой они появились, изменяет свой состав. При температуре 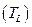в равновесии будут находится кристаллы твердого раствора состава точки 2 и жидкость состава точки 3. Концентрацию веществ в каждой фазе определяем по оси состава диаграммы, для чего проектируем на нее точки 2 и 3. Понижая температуру, получаем для каждого конкретного случая соответствующие фазовые равновесия. Так, при 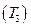в равновесии находятся кристаллы состава точки 4 и жидкость состава точки 5. Когда температура достигает 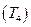жидкость приобретает состав точки Э. Эта жидкость получила название эвтектической, ее главным свойством является то, что из этой жидкости при охлаждении всегда образуются две новые фазы со средним составом, отвечающим точке Э. Процесс затвердевания такой жидкости происходит также, как у чистых веществ, при постоянной температуре. Из эвтектической жидкости в нашем случае при Т одновременно выделяются механическая смесь твердых кристаллов 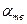и .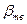

При всех температурах ниже 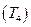в равновесии будут находиться друг с другом только кристаллы разных по составу фаз.

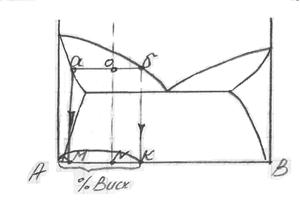По диаграмме плавкости можно определить массу равновесных фаз и зная их процентный состав, можно осуществить материальный баланс на любой из стадий охлаждения или нагрева. При этом применяют, так называемое правило “рычага” (правило отрезков).

Для вывода правила рычага составим уравнение материального баланса. Материальный баланс по компоненту В заключается в следующем:

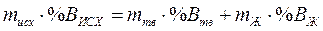
Преобразуем уравнение к виду:

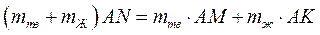
откуда получим:

В итоге или

Откуда получим

Уравнение (1) позволяет определить соотношение между массами равновесных фаз. Чтобы знать абсолютную массу, необходимо знать m_исх., тогда: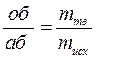

Таким образом, видим, что если рассматривать жидкость точки б, то ее массе пропорционален отрезок АО, если рассматривать кристаллы точки а – то отрезок об.

Величина отрезков ао и об измеряют линейкой на диаграмме состояния, учитывая состав исходной жидкости и температуру.