КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Статистические приемы анализа
- Сравнения– прием, позволяющий дать характеристику явления через однородн явления: факт и план одного п-да; факты отчетного и прошлого п-да; план предстоящ и факт прошл п-да; межцеховое сравнение; сравнение с лучшими предприятиями.
- Абсолютные и относительные величины.
Относительная величина – рез-т сравнения абсолютных чисел друг с другом. Формой выражения является коэффициент или процент.
относительная величина выполнения плана =
Примен при анализе выполнения плана.
- Средние величины. Среднее это обобщающий показатель, характеризующий значение признака в расчете на единицу совокупности.
Средн арифм простая - 
.Средн арифм взвешенная -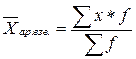 
Средняя геометрическая - 
, где n – число уровней.
Средняя хронологическая - 
, у1, у2 – уровни по сост-ю на дату.
- Показатели вариации отражают меру отклонений отдельных вариантов от средней величины.
размах вариации R = xmax-xmin
среднее линейное отклонение 
, 
Показывает насколько в среднем отклоняются отдельные варианты от их средней величины.
Дисперсия – средний квадрат отклонений 
, 
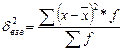
Коэффициент вариации 
, 
Показывает насколько процентов в среднем отклоняются отдельные варианты от их средней величины.
- Показатели динамики
абсолютный прирост П=уi-yi-1 (цепной способ), П=уi-yбаз (базисный способ)
темп роста = уi /yi-1 – цепной способ, Тр= уi /yбаз
Темп прироста =Тр-1, Тпр(%)=Тр(%)-100, Тпр=П/уi-1
Абсолютное значение одного процента прироста =П/Тпр(%)
Средний абсол прирост 
, n – число приростов.
Средний темп роста 
, 
, n – число темпов
Средний темп прироста 
- Индексы – особые относительные величины, в зависимости от обхвата единиц совокупности они бывают: индивидуальные и общие. Общие в зависимости от методики построения делятся на: агрегатные и средние из индивидуальных. Агрегатные на: объемных и качественных показателей.
Индивидуальные индексы – обычная относительная величина, характеризующая изменение единицы совокупности. 
Общие индексы отражают изменение сложных явлений, состоящих из величин неподдающихся суммированию.
К объемным относят общий индекс товарооборота: 
; 
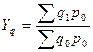
Агрегатный качественных показателей: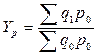 
; 
Средние из индивидуальных – любой агрегатный индекс и вместо индексируемого (изменяющегося) показателя ставят его значение, выведенное из формулы индивидуального индекса:
Jq=∑q0tqp0/∑q0p0 – средний арифметический индекс физического объема.
Jq=∑q1p0/∑q0p0/tq – средний гармонический индекс физического объема.
Дата добавления: 2015-04-21; просмотров: 72; Мы поможем в написании вашей работы!; Нарушение авторских прав |