Основные типы ограничений

Построение базовых элементов

К базовым элементам относятся главным образом точка, отрезок прямой, прямая, дуга окружности, окружность, лекальная кривая, текст, контур.

Непосредственное задание с использованием выбранного синтаксиса представления

При этом способе задания базовых элементов выбирается синтаксис их описания. Он может быть строго ограничен для каждого элемента или иметь несколько вариаций. Пользователь выбирает наиболее удобную для конкретного применения. И в соответствии с этим вводятся параметры элементов.

Например, отрезок может быть задан двумя точками. Точка п.с. пару координат (x и y); окружность — т. центра и радиус и т.д.

Пример - AutoCad.

С помощью уравнений

Базовые элементы задаются с помощью уравнений. Общее решение построения можно получить в 2 этапа:

1) составляя систему алгебраических уравнений (на основе типов ограничений, элементов и параметров)

2) решая эту систему (значения, характеризующие искомый элемент, принадлежат множеству решений системы уравнений)

Очевидным достоинством этого способа является его общность, т.к. для добавления нового ограничения достаточно написать соответствующие уравнения.

Недостаток — система уравнений может оказаться нелинейной. Поэтому требуются упрощения, а в некоторых случаях — интерактивный режим для нахождения приближенного решения.

С помощью ограничений

Построение при ограничениях применяется к объекту. Ограничение определяется следующим образом:

(тип элемента для построения)((список ограничений), (тип элемента, к которому относятся ограничения))

Основные типы ограничений

1) Проходит через n точек

2) Касается n объектов

3) Параллельно другому объекту

4) Образует некоторый угол с объектом

5) Отстоит от другого объекта на некотором расстоянии

Достоинство этого способа состоит в том, что не приходиться прибегать к очень сложным методам вычислений. Поиск решений полностью управляем. Кроме того можно организовать библиотеку подпрограмм для каждого применения.

Недостаток — для добавления нового ограничения или нового типа элемента надо писать новые подпрограммы.

Пример — построить окружность, касательную к заданным прямой и окружности, если известны R искомой окружности и примерное положение ее центра.

В зависимости от расположения заданных прямой и окружности, искомая окружность может размещаться следующим образом:

Рис. 7.1

После выбранного способа анализируется примерное положение центра искомой окружности. Такая последовательность действий приводит в итоге к однозначному решению.

С использованием геометрических преобразований

Новые элементы можно получать, выполняя геометрические преобразования (перенос, поворот, масштабирование) над уже имеющимися элементами или объектами.

1. Примеры двумерных моделей.

Техническое черчение

Под техническим черчением в данном случае понимается использование методов, аналогичных тем, которые традиционно применяются чертежниками, но с использованием средств информатики (дисплеи, средства диалога). Соответствующее ПО для компьютера дает возможность формировать и изменять (часто в интерактивном режиме) чертежи. Такой вариант модели представляет в расположение пользователя лишь совокупность двумерных элементов (обычно — отрезки и дуги).

В модели содержится только 1 вид объекта, что соответствует очень низкому уровню знаний о нем. Если сформировать несколько видов, то как правило в модели не представлены возможные отношения между видами. Поэтому всякое изменение в одном виде не находит отражения в других видах.

Параметризация

Этот метод строится на основе понятия “семейство деталей”. Под “семейством деталей” понимают набор деталей, состоящих из одинаковых элементов и различающихся лишь значениями некоторых параметров (в данном случае геометрических).

Цепное кодирование

Этот способ позволяет представить линейный чертеж в детализированном виде на клетчатой поверхности. В результате дискретизации кривая описывается последовательностью коротких элементарных векторов, ориентированным по восьми направлениям.

1. 3-мерное моделирование. Типы данных.

Типы данных:

1) Элементы нулевого уровня, то есть двумерные элементы (точки, отрезки, окружности, дуги, кривые, контуры).

2) Элементы первого уровня, то есть поверхности (плоскости, линейчатые поверхности, поверхности вращения, криволинейные поверхности).

3) Элементы второго уровня, то есть объемы (цилиндры, конусы, призмы…, произвольные многоугольники, произвольные объемы).

Из этих элементов с помощью различных операций можно создавать комплексы. Мы уже говорили, построение объемной модели может быть осуществлено двумя методами:

1) представление объекта с помощью границ (грани, ребра, вершины);

2) представление с помощью дерева построения (узлы представляют собой операции, листья — базовые объекты).

Представление с помощью границ

Для простоты рассмотрим случай представления объекта в виде совокупности плоских граней, ограниченных ребрами, которые в свою очередь ограничены вершинами.

В этом случае используются данные трех типов:

1) геометрические (координаты вершин, уравнения ребер или поверхностей);

2) топологические (связь между геометрическими данными);

3) вспомогательные (атрибуты данных, напр., цвет грани, степень ее прозрачности).

Топологические и геометрические данные, как правило, не смешивают. В их разделении есть свои достоинства. Например, если надо перенести объект, то координаты вершин умножают на матрицу переноса. Топология объекта остается без изменения.

Рассмотрим первую модель, достаточно низкого уровня, так как хранятся только ребра и вершины (каркасная модель):

Рис. 8.1

Рассмотрим вторую модель, более высокого уровня. В ней топологические и геометрические данные полностью разделены. Дана также информация о связи между ребрами, связи между гранями и уравнения граней, что дает значительные дополнительные возможности при работе с такой моделью:

Рис. 8.2

Представление с помощью дерева

В качестве базовых элементов используются часто элементарные сплошные тела. Деталь мысленно разбивается на элементы, модели которых уже имеются в системе.

Обычно используются следующие операции:

¾ объединение;

¾ пересечение;

¾ вычитание.

Упрощенным вариантом этой модели может быть случай, когда надо разместить некоторое число тел, что часто случается при архитектурном проектировании, при выполнении планировки цеха.

1. Методы описания 3-мерных моделей.

Возможны следующие методы описания трехмерных объектов:

Описание геометрии объекта с использованием алфавитно-цифрового входного языка

В большинстве систем, оперирующих с элементарными объемами, конструирование изделий происходит последовательно, по принципу агрегатирования. Определение элементарных объемов и их синтез проводятся с использованием формализованного языка. С его помощью можно описать размеры элементарных объемов, способ из соединения, установку системы координат и так далее. Формализованный язык может содержать не только геометрические параметры, но и информацию конструктивного и технологического плана (простановка размеров, шероховатость поверхностей, отклонения, допуска …).

Использование элементарных объемов снижает затраты на описание объекта, так как нет необходимости описывать отдельные контуры или поверхности, они определяются с помощью одного оператора входного языка.

Недостаток — пользователю надо освоить специфику используемого формализованного языка.

Описание объекта в режиме графического диалога

Это возможно только при наличии соответствующих технических средств — дисплеев для генерации динамических изображений и устройств ввода графической информации.

Пример. Создание в AutoCadе библиотеки КЭ с помощью блоков. Конструирование осуществляется в диалоге путем соединения КЭ с нужными размерами.

Получение модели объекта путем ввода эскизов и восстановлением модели по имеющимся проекциям

Этот метод соответствует традиционным методом конструирования и осуществляется в два этапа:

1) ввод эскизов;

2) восстановление модели;

Для решения таких задач в структуре программного модуля предусмотрены специальные процессоры:

1) Пц для обработки эскизов (осуществляет ввод эскизов и на их основе формирует точный контур);

2) Пц восстановления (создает проекции и по ним генерирует объемную модель);

3) Пц генерации изображения (осуществляет графический вывод точного контура, проекций, проволочной и объемной моделей).

Ввод эскизов и их обработка предполагают наличие соответствующего технического и программного обеспечения. В качестве устройства ввода графической информации можно использовать специальное графическое устройство, в котором поверхность съема информации разделена на части для вычерчивания фронтальной, профильной и горизонтальной проекций.

1. Методы построения 3D моделей (построение кривых и пов-тей, кусочно-аналитическое описание, кинематический принцип).

Построение кривых и поверхностей

Способы построения кривой:

¾ интерполяция по точкам;

¾ деформация кривой (перемещение точки, изменение полинома);

¾ вычисление эквидистанты к заданной кривой;

¾ формирование кривой из отрезков и дуг;

¾ вычисление различных сечений;

¾ пересечение поверхностей.

Способы построения поверхности:

¾интерполяция по точкам;

¾деформация поверхности;

¾перемещение образующей кривой по заданной траектории;

¾вычисление эквидистантой поверхности на заданном расстоянии.

Задание гранями (кусочно-аналитическое описание)

Модель представляет собой пятиуровневую иерархическую структуру. Тело представляется множеством ограничивающих его граней: . Каждая грань задается множеством ограничивающих ее ребер: и нормалью , направленной из тела; каждое ребро — двумя точками: ; и каждая точка — тремя координатами: 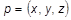. Для реализации аналитических операций над гранями, для каждой грани задаются 4 коэффициента — A, B, C, D, однозначно определяющие уравнение плоскости.

Модель может быть реализована в виде графа:

Рис. 8.11

Можно определить, какой объем памяти нужен для хранения этой модели в машинных словах. Считаем, что для записи одной ссылки и одного числа используется одно машинное слово.

Координаты вершин — 24 слова.

Коэффициенты уравнений плоскостей граней — 24 слова.

Ссылки первого уровня — 6 слов.

Ссылки второго уровня — 24 слова.

Ссылки третьего уровня — 24 слова.

Ссылки пятого уровня — 24 слова.

Итого — 126 слов.

Кинематический принцип

Задание толщиной:

.

Контур С, помещенный в плоскости Р порождает тело S путем переноса по направлению D на расстояние L.

Рис. 8.12

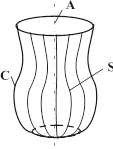
Задание вращением

Тело получается путем вращения контура С вокруг оси А.

Рис. 8.13

1. Методы построения 3D моделей (булевы операции).

Булевы операции

Модель представляет собой дерево, узлы которого — операции, листья — базовые элементы. Каждый базовый элемент имеет свою геометрию и топологию и представлен в виде геометрической модели (каркасной, поверхностной, объемной).

При вызове базового элемента для присоединения к объекту он должен в общем случае обладать следующими атрибутами:

где — координаты точки привязки ЛСК и ГСК; — углы поворота ЛСК относительно ГСК; — параметры элемента.

В некоторых ситуациях задача может упрощаться. Например, при конструировании тела вращения (вала) отпадает надобность в задании углов и точки привязки, так как элементы соединяются строго по оси друг за другом. В таком случае необходима информация только о параметрах элементов.

Чаще всего при конструировании объекта используются следующие операции над базовыми элементами:

¾объединение;

¾пересечение;

¾разность.

В настоящее время существует два метода геометрического объединения:

1) метод контактного соединения;

2) метод соединения с проникновением.

Метод контактного соединения применяется при наличии у тел плоских поверхностей, по которым они могут быть соединены. Далее проводится анализ граничных контуров поверхностей, по которым соединяются тела. Существует много разных методик, но общими действиями обычно остаются:

¾аналитическое описание граничных контуров двух тел;

¾определение точек пересечения контуров и их сегментация;

¾анализ вершин.

Метод контактного соединения прост в реализации. Затраты на программирование и время обработки программ невелики.

Метод соединения с проникновением. В данном случае используются не контурные плоские элементы, а поверхностные и соответственно рассчитываются кривые пересечения. Расчет кривых пересечения требует больших затрат, так как для каждой комбинации поверхностей надо разрабатывать свой алгоритм вычисления кривой пересечения.

Обычно существует два пути:

1) когда поверхности заданы аналитически (но тогда есть ограничение — поверхности должны быть максимум второго порядка);

2) численное определение кривой пересечения.

Этапы метода соединения с проникновением.

Этап 1. Определение объемов V1 и V2 на основе математического представления поверхностей, образующих эти объемы.

Рис. 8.14

Этап 2. Определение пар потенциально пересекающихся поверхностей (F1 и F2).

Рис. 8.15

Этап 3. Аналитическое определение кривой пересечения для пары пересекающихся поверхностей и удаление тех сегментов кривой, которые не лежат внутри пересекающихся поверхностей.

Рис 8.16

Этап 4. Сегментация поверхности в соответствии с полученной кривой

.

Рис. 8.17

Этап 5. Удаление сегментов поверхностей.

Рассмотрев другую пару поверхностей, получим:

Рис. 8.18

1. Методы построения 3D моделей (полигональные сетки).

Рис. 8.19. Поперечное сечение криволинейного объекта и его полигональная аппроксимация

Полигональной сеткой называют совокупность связанных между собой плоских многоугольников, с помощью которых можно аппроксимировать сложные криволинейные поверхности. Недостаток метода — его приблизительность.

Для улучшения качества можно увеличить число многоугольников для аппроксимации, но это приведет к дополнительным затратам памяти и вычислительного времени.

Явное задание многоугольников

Каждый многоугольник можно задать в виде списка координат его вершин:

.

Вершины запоминаются в том порядке, в котором они встречаются при обходе вокруг многоугольника. При этом все последовательные вершины, а также первая и последняя соединяются ребрами. Для каждого отдельного многоугольника данный способ записи является эффективным, но для полигональной сетки дает большие потери памяти вследствие дублирования информации о координатах общих вершин (недостаток 1). Кроме того, нет явного описания общих ребер и вершин. Например, поиск всех многоугольников, имеющих общую вершину, требует сравнения троек координат одного многоугольника с тройками координат всех остальных многоугольников (недостаток 2). Наиболее эффективный способ выполнить такое сравнение — сортировка всех N троек координат: для этого потребуется в лучшем случае — сравнений. Но и при этом существует опасность, что одна и та же вершина вследствие ошибок округления может в разных многоугольниках иметь различные значения координат, поэтому правильное соответствие может быть никогда не найдено.

Полигональная сетка изображается путем вычерчивания ребер каждого многоугольника, однако это приводит к тому, что общие ребра рисуются дважды (недостаток 3).

Задание многоугольников с помощью указателей на вершины

Каждый узел запоминается лишь один раз в списке вершин

.

Многоугольник определяется списком указателей на вершины. Например:

Рис. 8.20

,

.

Общие ребра рисуются дважды (недостаток).

Явное задание ребер

В этом представлении есть список вершин:

,

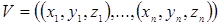и список ребер, где каждое ребро указывает:

,

Рис. 8.21

на две вершины в списке вершин, определяющие это ребра, а также на один или два многоугольника, которым это ребро принадлежит. Если ребро принадлежит одному многоугольнику, то либо Р1, либо Р2 — пусто.

,

,

, .

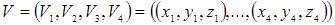Полигональная сетка изображается путем вычерчивания не всех многоугольников, а всех ребер. В результате многократной отрисовки ребер не происходит.

1. Описание поверхностей (параметрическое, неявными функциями, поточечное).

Параметрическое описание

Поверхности, заданные в виде:

,

где u,t – параметры, изменяющиеся в заданных пределах, относятся к классу параметрических.

Для одной фиксированной пары (u,t) можно вычислить положение только одной точки поверхности. Для полного представления всей поверхности необходимо с определенным шагом перебрать множество пар (u,t) из диапазона их изменений, вычисляя при этом X,Y,Z.

Плоскость, проходящая через точку (x0,y0,z0) и векторы и , исходящие из этой точки, определяется:

,

где - проекции (m=1,2) на оси OX,OY,OZ.

Приведенное уравнение опишет прямоугольник со сторонами длиной и , если единичные векторы и будут перпендикулярны друг другу, а параметры u и t изменяются от 0 до1.

Нормаль к плоскости, заданной параметрически, может быть определена как:

.

Эллипсоид вида:

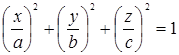
в параметрическом виде запишется:

, -долгота, — ширина.

Неявное описание типа 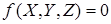этих и многих других поверхностей невозможно.

¾ Приспособленность к физическим процессам управления резцом в станках с ЧПУ. Резец должен вытачивать деталь, двигаясь в пространстве по законам, заданным в параметрической модели.

¾ Параметрические поверхности легко ограничиваются в пространстве пределами изменения параметров. Например, наружная поверхность дольки апельсина в виде 1/8 шара радиуса r:

¾

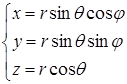, где , .

Описание неявными функциями

Заключается в моделировании поверхностей в виде:

.

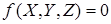Могут быть использованы функции различных порядков, но из-за сложности математической обработки ограничиваются 1-ой и 2-ой степенью. Поверхности, описываемые функциями 3-ей и 4-ой степени, незначительно расширяют возможности геометрической имитации форм, а вычисления резко увеличиваются.

Поточечное описание

Поверхность представляется множеством отдельных точек, принадлежащих этой поверхности. Теоретически, при бесконечном увеличении числа точек, такая модель обеспечивает непрерывную форму описания.

Поточечное описание применяют в случаях, когда поверхность очень сложна, не обладает гладкостью, а детальное представление многочисленных геометрических особенностей важно. Например, участки грунта на других планетах, формы малых небесных тел, информация о которых доставлена с искусственного спутника в виде нескольких стереопар; микрообъекты, снятые с помощью микроскопов.

Исходная информация представляется в виде матрицы 3-хмерных координат точек. Они определяются автоматизированными методами на стереоприборах. Часто используется сопоставление стереопар. Надо учитывать требуемую частоту расположения точек.

1. Характеристики поверхностей (1-го порядка, 2-го порядка).

Поверхности 1-го порядка

Поверхности вида:

в матричном виде имеют вид:

, где .

Изменяя компоненты матрицы Р можно описать плоскость любой ориентации и положения, это будет бесконечная плоскость. Реальный участок имеет ограничения. Наиболее удобно ограничение выпуклым многоугольником. Все другие случаи, как криволинейного ограничения, так и невыпуклой фигурой, могут быть сведены к первому путем аппроксимации или разбиения на выпуклые подфигуры. Рассмотрим крыло самолета.

Граничные точки многоугольника однозначно оцифровывают и записывают их координаты в матрицу:

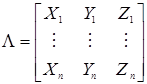, где .

Уравнение плоскости определяют на основе трех точек, не лежащих на одной прямой:

.

Нормаль : .

Направлена нормаль в сторону полупространства, где значение скалярного поля .

Из поверхностей первого порядка составляются полигональные сетки (серия смежных многоугольников, не имеющих разрывов между собой; каждое ребро является общим для смежных многоугольников).

Описывающая функция обладает непрерывностью, а производная имеет разрывы в местах стыка участков.

Достоинства:

— простота обработки.

Поверхности 2-го порядка

Все поверхности кроме эллипсоида бесконечны. Поэтому только эллипсоид может самостоятельно образовывать объемный примитив, все другие требуют ограничения в пространстве.

Квадратичная функция в матричном виде:

, где .

Нормаль к поверхности в точке (X,Y,Z) определяется:

, где ,

i, j, k – орты осей OX,OY,OZ. Направлена нормаль по градиенту скалярного поля , то есть в сторону увеличения значений . Так как функция является монотонной и однократно знакопеременной, то направлена в ту часть подпространства, где . Например, к поверхности шара направлена внутрь шара, а к поверхности того же шара направлена наружу.

1. Использование фракталов.

Фрактальные поверхности

Естественные сцены часто не может быть описаны на основе традиционных приемов, базирующихся на использовании непрерывных функций. Но можно заметить, что большинство природных сцен статически родственны. Проведя анализ нерегулярных изображений береговой линии, полученных при съемке с высот 10; 3 км и при наблюдении с поверхности земли, было установлено, что при любом уровне разрешения береговая линия может быть смоделирована и нарисована посредством объединения участков небольших прямолинейных сегментов. Причем при переходе на каждый следующий, более высокий уровень разрешения, который был аппроксимирован первым прямолинейным сегментом, этот сегмент вероятностным способом разбивается на последовательность линейных сегментов, и т.д. На основании этого свойства – постоянства статистического закона порождения деталей природных образований при переходе от низких к более высоким уровням разрешения – построен метод использования фрактальных поверхностей.

В переводе (англ.) “фрактальный” обозначает состоящий из частей. Такими поверхностями называется класс нерегулярных геометрических форм, задаваемых вероятностным образом на основе исходного описания низкого разрешения. Случайный закон, по которому исходная линия или поверхность дробится на несколько более мелких, подбирается опытным путем по критерию визуального согласования синтезированного изображения с реальной сценой.

Часто фрактальные поверхности используются для моделирования горного ландшафта. Вначале горный массив описывают очень приближенно полигональной сеткой из четырехугольников. Каждый четырехугольник разбивают с помощью случайной функции на 4 фигуры меньших размеров, причем эти фигуры вероятностным образом сдвигают относительно плоскости исходного четырехугольника, сохраняя для каждой фигуры по одной общей вершине с исходным четырехугольником. Каждую фигуру вновь делят и так до достижения желаемого уровня изрезанности поверхности. Далее удаляются скрытые линии и производится закраска четырехугольников. Изображения, созданные на основе фрактальных поверхностей, только статистически идентичны реальным объектам и не обладают идеальной точностью.

1. Деформация 3-х мерных объектов.

Деформация (или морфинг) трехмерных объектов — это большая область компьютерной графики, в которой решаются задачи преобразования геометрических характеристик объектов. Примеры задач из этой области:

¾ «превращение» трехмерных объектов друг в друга;

¾ анимация — построение промежуточных модификаций объекта (морфопоследовательности) по двум крайним, причем каждая модификация может отличаться как пространственным положением, так и формой;

¾ произвольная деформация объекта с целью получения новых геометрических форм;

¾ моделирование неупругого взаимодействия физических тел;

¾ моделирование роста биологических объектов и т.д.

Конкретный алгоритм, по которому осуществляется деформация, сильно зависит от способа задания объекта.

К настоящему времени разработано большое количество методов трехмерной деформации, отличающихся по способу задания деформируемых объектов, степени физической достоверности моделируемого изменения формы (здесь имеется в виду соответствие наблюдаемой картины физическим законам) и, конечно, по производительности или по скорости работы. Как правило, деформация тел на основе физических законов требует больших вычислительных затрат, чем свободная деформация, т. е. рассчитываемая без учета физических свойств объекта и влияния других тел.

1. Методы создания реалистических 3-х мерных изображений.

Главная трудность на пути получения изображения объекта состоит в том, что все устройства вывода является двумерными. Трехмерные объекты приходится проецировать на плоскость, что приводит к существенным потерям информации, а иногда и к неопределенности изображения. Мы рассмотрим методы, которые используются для восстановления информации, которая теряется при проецировании (пример с кубом).

Рис. 10.1

С середины 60-х годов ведутся поиски способов и средств создания реалистичных изображений, чтобы наблюдатель принимал изображение за реальный объект, а не за синтетический объект, существующий только в памяти ЭВМ. Это особенно важно при моделировании, проектировании, организации досуга.

Конструкторам автомобилей, самолетов, машин и т.д. хотелось бы заранее знать, как будет выглядеть их проект. Формирование реалистичных изображений, сгенерированных на ЭВМ, во многих случаях представляет собой легкий, дешевый и более эффективный способ наблюдения предварительных результатов, чем изготовление моделей и опытных образцов, кроме того, он позволяет рассмотреть большее число вариантов проекта.

Основной трудностью создания реалистичных изображений является сложность реальных визуальных образов. Наше окружение очень разнообразно. В нем существуют многочисленные фактуры поверхности, плавные переходы цветов, тени, отражения и мелкие неровности (царапины на полу, чешуйки краски, выступы на стенах). Сочетаясь в нашем сознании, они образуют «реальный» визуальный опыт.

Главная трудность при изображении пространственных отношений — практически все устройства вывода является двумерными. Следовательно, трехмерные объекты приходится проецировать на плоскость, что приводит к существенным потерям информации, а иногда к неопределенности изображения.

Рассмотрим методы, которые используются для восстановления информации, чтобы присущие человеку механизмы восприятия глубины могли соответствующим образом ликвидировать неясности.

Рис. 10.2

Перспективные проекции

Размеры объектов обратно пропорциональны их расстоянию от наблюдателя. Меньший объект расположен дальше. Но перспектива подходит не всегда. Особенно эффективно ее использование для объектов с большим числом параллельных линий, так как на изображении они будут сходиться в точке схода. Фактически это схождение линий лучше передает глубину, чем уменьшение размеров. Для сложных объектов (молекулярные структуры), где отсутствуют параллельные линии, перспективные изображения мало пригодны.

Рис. 10.3

Передача глубины яркостью

Глубину объекта (расстояние до него) можно представить путем изменения уровня яркости: объекты, находящиеся ближе к наблюдателю, должны выводиться с увеличенной яркостью. Для реализации этого принципа необходима информация о глубине (координате z). Но человеческий глаз различает яркости гораздо хуже, чем положение по глубине, поэтому передать небольшие различия в расстояниях с помощью яркости сложно.

Аналогия с реальным зрением.

Отсечение по глубине

Выводимый объект пересекается плоскостью, отсекающей его удаленную часть. Удобно динамически изменять положение отсекающей плоскости.

Динамические проекции

Если серию проекций объекта выводить быстро с разных точек зрения, расположенных недалеко друг от друга, то создается впечатление вращения объекта. Метод эффективен, но надо специальное аппаратное обеспечение.

Удаление скрытых линий и поверхностей

Эти алгоритмы требуют больших затрат машинного времени и не удовлетворяют требованиям относительно времени ответа в машинной графике. Поэтому они используются часто как дополнительная возможность, и пользователь применяет ее очень экономно.

Стереоскопия

Если посмотреть на объект поочередно одним и другим глазом, то два вида будут при этом различаться (бинокулярный эффект). Наш мозг сливает два раздельных образа в один трехмерный. Два изображения можно объединить в один трехмерный образ, если разглядывать эту пару так, чтобы каждый глаз видел только одно изображение. Разработчик интерактивной системы должен предъявить каждому глазу вид, который отличается от другого.

Используется шлем с двумя ЭЛТ. При движении головы может изменяться и изображение (датчики, фиксирующие движение).

1. Получение проекций. Основные виды проекций.

В общем случае проекции преобразуют точки в СК размерностью n в точки СК размерностью m, где m<n. Мы рассмотрим преобразование 3-хмерного пространства в 2-мерное.

Проецирование 3-хмерного объекта осуществляется при помощи прямых проецирующих лучей, которые называются проекторами и которые выходят из центра проекции, проходят через каждую точку объекта и, пересекая картинную плоскость, образуют проекцию. Т.к. проекция отрезка сама является отрезком, то достаточно спроектировать лишь конечные точки.

Рис. 11.1

Определенные т.о. проекции являются плоскими геометрическими проекциями (проецирование на плоскость прямыми линиями).

Рис. 11.2

Если расстояние между центром проекции и плоскостью проекции конечно, то проекция называется центральной, если же бесконечно, проекция – параллельная.

При описании центральной проекции (ЦПр) задается центр проекции, а при описании параллельной проекции (ППр) – направление проецирования.

Параллельные проекции

ППр делятся на 2 типа в зависимости от соотношения между направлением проецирования ( ) и нормалью к проецируемой плоскости ( ).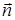

— В прямоугольных проекциях эти направления совпадают ( ), а в косоугольных — нет ( ). Наиболее широко используются ортографические проекции: вид спереди, сверху и сбоку, в которых картинная плоскость перпендикулярна главным координатным осям, совпадающим с направлением проецирования .

Рис. 11.3

В аксонометрических проекциях используется проекционная плоскость, не перпендикулярная главным координатным осям, поэтому на них изображается сразу несколько сторон объекта. Сохраняется параллельность прямых, а углы изменяются.

Широко используется изометрия. В этом случае нормаль к проекционной плоскости составляет равные углы с каждой из главных координатных осей. Если нормаль к проекционной плоскости имеет координаты (а,в,с), то |a|=|в|=|с|.

Существует 4 различные изометрические проекции: (а,а,а); (-а,а,а); (а,-а,а);

(а,а,-а). (Остальные 4 варианта дублируют эти, т.к. (а,а,а)=(-а,-а,-а)).

Свойство изометрии: все 3 главные координатные оси одинаково укорачиваются.

в диметрии нормаль к проекционной плоскости составляет равные углы с двумя координатными осями.

В триметрии нормаль Пр-ой плоскости образует с координатными осями различные углы.

— Косоугольные проекции ( ) сочетают в себе свойства ортографических проекций со свойствами аксонометрии. Проекционная плоскость перпендикулярна главной координатной оси, поэтому сторона объекта, параллельная этой плоскости, Проецируется так, что углы и расстояние не искажаются.

В косоугольной изометрии направление проецирования составляет с проекционной плоскостью угол 450. В результате проекция отрезка, перпендикулярного проекционной плоскости, имеет ту же длину, что и сам отрезок, т.е. укорачивания нет.

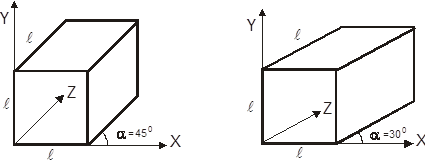
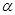
обычно = 300 или 450

Рис. 11.4

В косоугольной диметрии направление проецирования составляет с проекционной плоскостью угол . Отрезки, перпендикулярные проекционной плоскости, после проецирования составляют 1/2 их действительной длины.

Рис. 11.5

Эта проекция более реалистична, т.к. укорачивание с больше согласуется с нашим визуальным опытом.

Центральные проекции

Основное свойство — более удаленные предметы изображаются в меньших масштабах.

Рис. 11.6

Параллельные прямые в общем случае на изображении не параллельны.

Если совокупность прямых параллельна одной из главных координатных осей, то их т. схода называется главной т. схода. Имеется 3 такие точки.

Если проекционная плоскость перпендикулярна оси Z, то лишь на этой оси будет лежать главная т. схода.

Центральные проекции классифицируется в зависимости от числа главных точек схода, которыми они обладают.

Рис. 11.7

2-точечная центральная проекция широко применяется в архитектурном, инженерном проектировании и в рекламных изображениях, в которых вертикальные прямые проецируются как параллельные.

3-хточечные центральные Пр почти совсем не используются, т. к. их трудно конструировать, и они добавляют мало нового с точки зрения реалистичности.

Перспективное изображение зависит от положения глаза. Эффект перспективы обратно пропорционален расстоянию между глазом и объектом. Если глаз находится близко от объекта, то получается сильный эффект перспективы (хорошо видны т. схода, линии явно не параллельны). Если глаз расположен далеко, то параллельные линии объекта будут казаться параллельными и на картинке.

1. Математическое описание параллельных проекций.

Ортографические проекции получаются достаточно просто. Если проекционная плоскость - Z=0, направление проецирования = оси Z, то точка Р

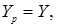
Матрица проецирования:

— фронтальная проекция

Аналогично для 2-х других проекций:

— профильная проекция

— горизонтальная проекция