Математическое описание косоугольных проекций

Матрица проецирования может быть записана исходя из значение 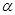и . Рассмотрим единичный куб, спроецированный на плоскость ХУ. Точка Р принадлежит объекту, а точка - изображению т. Р на рисунке.

Рис. 11.8

Проекцией точки Р(0,0,1) является т. ,принадлежащая плоскости ХУ. По определению это означает, что направление проецирования совпадает с отрезком . Это направление есть:

.

Направление проецирования составляет угол с плоскостью ХУ.

Рассмотрим произвольную т.(x,y,z) и определим ее косоугольную проекцию ( ) на плоскость ХУ.

Рис. 11.9

Уравнение для х и у – координат проектора как функций Z имеют вид

- (прямая 1, рис.1)

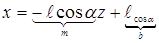- (прямая 2, рис.1)

На рис. 11.9 показаны 2 изображения т. и проектор, параллельный проектору на рис.11.9. Уравнения для х и у – координат проектора:

Находим , :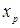

Матрица, которая выполняет эти действия, а следовательно описывает косоугольную проекцию:

Применение матрицы приводит к сдвигу и последующему проецированию объекта. Плоскости с постоянной координатой z=z1 переносятся в направлении х на , в направлении y — на и затем проецируется на плоскость z=0. Сдвиг сохраняет параллельность прямых, а также углы и расстояния в плоскостях, параллельных оси z.

Для изометрической косоугольной проекции (см. рис.11.9)

Для диметрической косоугольной проекции .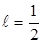

Для ортографической косоугольной проекции , .