
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аксонометрическая проекция
Получается при повороте на угол  относительно оси У и на угол
относительно оси У и на угол  относительно оси Х с последующим проецированием вдоль оси Z.
относительно оси Х с последующим проецированием вдоль оси Z.
Матрица проецирования:

Покажем, как при это преобразуется единичные орты координатных осей Х, У, Z:



Для изомерии:


Для диметрии:

- Математическое описание перспективных проекций.
Для простоты примем, что плоскость проецирования перпендикулярна оси z и совпадает с плоскостью z=d.

Рис. 11.10
Для каждой т. Р объекта т. изображения  определяется как т. пересечения прямой линии ОР и экрана.
определяется как т. пересечения прямой линии ОР и экрана.
Рассмотрим подобные треугольники:




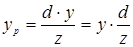
Расстояние d является в данном случае масшт-ым k. Фактором, приводящим к тому, что удаленные объекты выглядят мельче, является деление на z. Допустимы все значения z, кроме z=0.


Замечание 1: Т.к. т. О (  оси z)
оси z)  находится в центре объекта, а ось z совпадает с
находится в центре объекта, а ось z совпадает с  , то т. Q тоже будет находиться приблизительно в центре изображения объекта. Если расположить начало координат экрана (плоскости проецирования) в нижнем левом углу, а размеры экрана: а – по горизонтали, b – по вертикали, то
, то т. Q тоже будет находиться приблизительно в центре изображения объекта. Если расположить начало координат экрана (плоскости проецирования) в нижнем левом углу, а размеры экрана: а – по горизонтали, b – по вертикали, то

 .
.
Замечание 2: Необходимо определить расстояние между т. наблюдения Е и экраном – d.

Рис. 11.11

Это выражение равно применимо для горизонтальных и вертикальных размеров. Его надо использовать лишь для приблизительной оценки d, т.к. 3-хмерный объект может иметь сложную форму и не всегда ясно, какие размеры надо включать в это уравнение.
Замечание 3: Особенность нашего глаза такова, что мы можем видеть только точки, расположенные внутри определенного конуса, ось которого совпадает с направлением взгляда ОЕ. Очень важный параметр этого конуса – угол  .
.
Глаз, как и камера допускает только такие значения угла  , которые не
, которые не  . При выборе
. При выборе 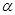 рекомендуется пользоваться формулой:
рекомендуется пользоваться формулой:
 .
.
Выбор слишком малого  может привести к трудностям. Если же
может привести к трудностям. Если же  будет слишком большим, то
будет слишком большим, то  будет мало, эффект перспективы уменьшится.
будет мало, эффект перспективы уменьшится.
Оптимальный вариант  .
.
Замечание 4: Рассмотрим случай, когда объект слишком длинный в направлении оси X (балка 200*2*2). Где лучше выбрать т. О? До сих пор мы выбирали ее в середине объекта. Всегда ли она будет и в центре объекта?

Рис. 11.12
Точка  , которая находится в центре изображения, не лежит на середине объекта.
, которая находится в центре изображения, не лежит на середине объекта.
Очевидно, что точка О надо выбирать не на середине балки, а ближе к глазу.
- Математическое описание произвольных проекций. Видовое преобразование.
В рассмотренных алгоритмах получения проекций были допущены ограничения на расположение картинной плоскости, центра проекции, что часто свойственно многим графическим пакетам.
Рассмотрим алгоритм получения проекций, когда картинная плоскость может располагаться относительно объекта произвольным образом. По сути дела задача сводится к преобразованию СК.

Рис. 11.13
Пусть объект задан в МСК, причем ее начало находится  в центре объекта (т. О). Объект наблюдается от точки Е к точке О. В точке Е расположим вторую СК – видовую СК. Вектор ЕО определяет направление наблюдения. Пусть точка Е задана в сферических координатах
в центре объекта (т. О). Объект наблюдается от точки Е к точке О. В точке Е расположим вторую СК – видовую СК. Вектор ЕО определяет направление наблюдения. Пусть точка Е задана в сферических координатах  по отношению к мировым. Т.е. ортогональные координаты
по отношению к мировым. Т.е. ортогональные координаты  могут быть вычислены:
могут быть вычислены:

Ось z ВСК расположена по линии наблюдения, x – вправо; y – вверх.
МСК – правосторонняя; ВСК – левосторонняя
(обычно так выбирается) (позволит определить картинные оси в тех же направлениях)

Рис. 11.14
Видовое преобразование:
 ,
,
где V – матрица видового преобразования (  ).
).
V представляет собой четыре элементарных преобразования и получается путем их перемножения.
Перенос
Перенос начала координат из точки О в точку Е.
Точка Е становится новым началом координат.

Поворот 1
Поворот СК вокруг оси z на угол  в отрицательном направлении (по часовой стрелке). В результате ось Y совпадает по направлению с горизонтальной составляющей отрезка ОЕ. Матрица такого изменения СК будет совпадать с матрицей для поворота точка на такой же угол в положительном направлении.
в отрицательном направлении (по часовой стрелке). В результате ось Y совпадает по направлению с горизонтальной составляющей отрезка ОЕ. Матрица такого изменения СК будет совпадать с матрицей для поворота точка на такой же угол в положительном направлении.

Поворот 2
Поворот СК вокруг оси X на угол  в положительном направлении, чтобы ось z совпадала по направлению с ОЕ. Этот поворот соответствует повороту т. на угол
в положительном направлении, чтобы ось z совпадала по направлению с ОЕ. Этот поворот соответствует повороту т. на угол  .
.

Изменение направления оси X
После 3-х преобразований оси Y и Z имеют правильную ориентацию, а ось X д.б. направлена в противоположную сторону:

Результирующая матрица

Теперь к полученным видовым координатам можно применить любое из элементарных проекционных преобразований (например, ортографическое, косоугольное или перспективное) для получения окончательного результата.
- Общие сведения об удалении скрытых линий. Сравнительная характеристика алгоритмов.
Общие сведения об удалении скрытых линий и поверхностей
Существует большое число способов решения этой задачи. Многие из них ориентированы на специализированное применение. Наилучшего решения задачи удаления скрытых линий и поверхностей не существует. Почти все алгоритмы удаления скрытых линий и поверхностей включают в себя сортировку по геометрическому расстоянию от тела до точки наблюдения. Основная идея сортировки — чем дальше объект, тем больше вероятность, что он будет заслонен другим объектом.
Все алгоритмы удаления скрытых линий и пов–тей можно разделить на два типа:
Алгоритмы, работающие в объектном пространстве (ОП) (каждая из n граней сравнивается с оставшимися n-1);
они имеют дело с физической СК, в которой описаны эти объекты;
весьма точны (полученные изображения можно легко увеличить в несколько раз);
объем вычислений теоретически n2;
Алгоритмы, работающие в пространстве изображения (ПИ) (надо определить, какая из n граней видно в каждой точке разрешения экрана), т.е. каждый объект сравнивается с каждым пикселем экрана:
имеют дело с СК экрана, на котором изображается;
точность ограничена разрешающей способностью экрана (если полученные результаты потом увеличивать во много раз, они не будут соответствовать исходному изображению);
объем вычислений теоретически — Nn (N=4000000—10000000) пикселей.
| Алгоритм | Число граней | ||
| Сортировка по глубине | |||
| z-буфер | |||
| Построчное сканирование | |||
| Разбиение области |
- Алгоритм сортировки по глубине.
Принцип: все объекты сортируются по глубине и выводятся на экран в обратном порядке, и таким образом, более близкие объекты затирают более дальние (алгоритм художника).
Шаги:
· Упорядочение всех объектов в соответствии с их большими z-координатами.

Рис. 12.1
· Разрешение всех неопределенностей, которые возникают при перекрытии z-оболочек (исследуется x-оболочка и y-оболочка).
· Преобразование каждого из объектов в растровую форму в порядке уменьшения z-координаты.
- Алгоритм, использующий Z-буфер.
Принцип: используются два буфера: регенерации, в котором хранятся значения  , z-буфер который хранит z-координаты.
, z-буфер который хранит z-координаты.
Буфер регенерации заполняется значениями при параллельном анализе z-координаты со значениями z-буфера.
Шаги:
· В z-буфере заносятся максимально возможные значения z;
· Буфер регенерации заполняется значениями фона;
· Каждый объект раскладывается в растр;
если  меньше значения z-буфера в элементе
меньше значения z-буфера в элементе  , то:
, то:
a)  заносится в элемент
заносится в элемент  z-буфера;
z-буфера;
b) значение  помещается в элемент
помещается в элемент  буфера регенерации.
буфера регенерации.
Сортировка не нужна.
Достоинства:
¾ простота реализации;
¾ нет сортировки.
Недостатки:
¾ нужен большой объем памяти для хранения z-буфера.
 Объем памяти: информация о значении
Объем памяти: информация о значении  — 24 бита (
— 24 бита (  ), информация о глубине 20 бит.
), информация о глубине 20 бит.
буфер регенерации  бит бит
| =1,5 Мбайт |
z-буфер  бит бит
|
¾ большая стоимость устранения лестничного эффекта.
Расчет координаты z:
Уравнение плоскости:
 ,
,  .
.
Если в точке  , то в точке
, то в точке  ,
,
где  ,
, 
Пример.

Рис. 12.2
Z — Б
I 
| БР

| Z — Б
II 
| БР

|
Z — Б
III 
| БР

| Z — Б
IV 
| БР

|
- Алгоритм построчного сканирования.
Принцип: расширение алгоритма преобразования многоугольника в растровую форму; разница в том, что имеем дело не с одним многоугольником, а со всеми сразу.
Шаги:
Создается таблица ребер (ТР). Она содержит все ребра многоугольников, отсортированные по меньшей y-координате.
Описание ребра содержит:

| 
| 
| Указание на многоугольник |
Создается таблица многоугольников (ТМ).
Описание многоугольников содержит:
| Коэффициенты уравнения плоскости (A, B, C, D) | Цвет |  Флаг = Флаг =
| 0 — вне |
| 1 — внутри |
Создается ТАР.
Содержит все активные ребра на текущей сканирующей строке. Ребра упорядочены по возрастанию x-координаты.

| 
| 
| Указание на многоугольник |
Пример.
Строка  — четыре ребра в ТАР.
— четыре ребра в ТАР.
 , флаг 1 = 1, флаг 2 = 0, извлекаем цвет 1.
, флаг 1 = 1, флаг 2 = 0, извлекаем цвет 1.

Рис. 12.3
 — —
| Флаг 2 = 0 |
| Флаг 1 = 0, цвет = фон |
 — —
| Флаг 2 = 1, цвет = цвет2 |
| Флаг 1 = 0; |
 — —
| Флаг 2 = 0, цвет = фон |
| Флаг 1 = 0; |
Строка  — четыре ребра в ТАР.
— четыре ребра в ТАР.
 — —
| Флаг 1 = 1, цвет = цвет1 |
| Флаг 2 = 0; |
 — —
| Флаг 1 = 1, |
| Флаг 2 = 1, вычисляется z1 и z2 из уравнений плоскости цвет = цвет 2 |
 — —
| Флаг 1 = 0, |
| Флаг 2 = 1, цвет = цвет2 |
 — —
| Флаг 1 = 0, цвет = фон |
| Флаг 2 = 0; |
Алгоритм немного усложняется, если многоугольники могут проникать друг в друга. Тогда находят линию пересечения и многоугольник разбивается на несколько.

Рис. 12.4
Удобно использовать принцип когерентности по глубине: если при переходе к следующей сканируемой строке ребра остаются те же и в том же порядке, то соотношения глубин остаются те же и их не надо вычислять.
- Алгоритм разбиения области.
В основе лежит гипотеза о способе обработки информации глазом и мозгом. Области, более насыщенные информацией, дальше приковывают к себе взгляд.
Широко используется когерентность (однородность смежных областей).
Принцип: область разбивается на окна и в каждом окне решается вопрос о том, пусто ли оно или достаточно просто для визуализации; если это не так, то окно разбивается дальше до тех пор, пока не станет простым или его размер не достигнет размера  .
.
При  надо максимально 9 разбиений.
надо максимально 9 разбиений.
Конкретная реализация алгоритма зависит от метода разбиения и критерия определения простоты изображения в окне.
Вариант 1:

Рис. 12.5
¾область разбивается последовательно на четыре равные прямоугольные части;
¾критерий простоты — объекты не попадают в область.
Вариант 2:
¾ критерий простоты — одна из четырех ситуаций:

Рис. 12.6
1. Не один многоугольник не пересекает область (цвет равен цвету фона);
2. Есть один внутренний или пересекающий многоугольник:
a) цвет равен цвету фона;
b) многоугольник раскладывается в растр со своим цветом;
3. Есть один охватывающий многоугольник (цвет равен цвету многоугольника);
4. Есть несколько внутренних, пересекающих многоугольников, и как минимум один охватывающий, расположенный ближе всех (цвет равен цвету охватывающего многоугольника).

Рис. 12.7
Меньше разбиений, но больше расчетов.
Вариант 3: область разбивается относительно вершин многоугольника.

Рис. 12.8
- Алгоритм плавающего горизонта. Алгоритм Робертса.
Используется чаще всего для удаления невидимых линий трехмерного представления функций, описывающих поверхности в виде:
 .
.
Подобные функции возникают во многих приложениях в математике, технике, естественных науках.
Трехмерная задача сводится к двумерной путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат x, y или z.

Рис. 12.9
На рисунке показаны параллельные плоскости с  . Функция
. Функция  сводится к последовательности кривых, лежащих в каждой из этих параллельных плоскостей, например, к последовательности:
сводится к последовательности кривых, лежащих в каждой из этих параллельных плоскостей, например, к последовательности:
 ,
,
где  на каждой из заданных параллельных плоскостей.
на каждой из заданных параллельных плоскостей.
Поверхность теперь складывается из последовательности кривых, лежащих в каждой из этих плоскостей (см. рис.).

Рис. 12.10
При проецировании кривых на плоскость z=0 (см. рис. 12.10) становится ясна идея алгоритма.
· В начале происходит упорядочивание плоскостей  по возрастанию расстояния до них от точки наблюдения.
по возрастанию расстояния до них от точки наблюдения.
· Для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней, то есть для каждого значения x в пространстве изображения определяется соответствующее y.
· Проверка: если на текущей плоскости при некотором значении x соответствующее значение y на кривой больше максимального или меньше минимального по y для всех предыдущих кривых при этом x, то текущая кривая видима, иначе — нет.

Рис. 12.11
Реализация алгоритма достаточна проста. Для хранения максимальных и минимальных значений y при каждом значении x используется два массива, длина которых равна разрешению по x. Значения в этих массивах представляют собой текущие значения верхнего и нижнего плавающего горизонта. По мере рисования каждой очередной кривой этот горизонт «всплывает».
Фактически этот алгоритм работает каждый раз с одной линией.
Дата добавления: 2015-04-18; просмотров: 233; Мы поможем в написании вашей работы!; Нарушение авторских прав |