Алгоритм Робертса 2 страница

Для программиста это означает то, что ему совсем не нужно прорисовывать изображение с точностью до мельчайших деталей. Большинство из этих деталей будет просто проигнорировано и "заполнено" чем - то другим. Ваша картина может быть значительно упрощена. Вот, например, в фильме "Возвращение Джедая" из знаменитых "Звездных Войн" один из космических кораблей в пространстве - это обыкновенный ботинок. Но никто этого не заметил, потому что ожидали видеть космический корабль, и в том месте действительно был объект, напоминающий его своей формой, поэтому все и видели именно космический корабль.

Вы можете еще более упростить свое конечное изображение, если сцена находится в движении. Нажмите паузу на видеомагнитофоне и посмотрите на неподвижное изображение, оно выглядит никуда негодным, но мы этого не замечаем, когда оно в движении.

Цель программиста, отвечающего за вывод графики в реальном времени, - обеспечить такие процедуры аппроксимации в визуализирующих фрагментах кода, которые улучшают реализм и точно передают атмосферу, дух создаваемого вами мира. Остальное пусть делает мозг. Цель программиста фотореалистичной графики - попытаться смоделировать взаимодействие света с объектами сцены настолько аккуратно, чтобы оно могло выдержать скрупулезную проверку человеческим мозгом.

Так же надо учитывать две особенности глаза:

1) Глаз приспосабливается к “средней” яркости сцены; поэтому область с постоянной яркостью на темном фоне кажется ярче или светлее, чем на светлом.

2) Еще одно важное свойство: границы областей постоянной яркости кажутся более яркими.

Рис. 13.1

Этот эффект является причиной слишком резкого перепада яркости на граничных ребрах, где происходит изменение яркости между соседними плоскостями. Это явление называется эффектом полос Маха.

На рис. показаны действительные и кажущиеся изменения яркости вдоль поверхности, вызванные литеральным торможением рецепторов глаза.

Рецепторы глаза при реакции на свет подвергаются воздействию соседних рецепторов.

Рецепторы, расположенные на границе перепада яркостей с более яркой ее стороны, подвергаются более сильному раздражению, чем те, которые находятся дальше от границы. Это объясняется тем, что они < затормаживаются своими соседями с более темной стороны. И наоборот, рецепторы, расположенные на границе с более темной стороны, подвергаются меньшему воздействию, чем находящиеся дальше от границы. Причина в том, что они подвергаются более сильному торможению от соседей с яркой стороны границы.

Эффект полос Маха мешает глазу создавать сглаженное изображение сцены. Увеличивая количество полигональных граней, его можно ослабить, но полностью уничтожить нельзя.

1. Модель освещения.

Свойства объектов

Отражающие свойства объектов описываются коэффициентами отражения, коэффициентом яркости и индикатрисой отражения.

В основу классификации объектов по характеру отражения падающего света положено пространственное распределение отраженного света. Определяющее влияние на характер распределения оказывает структура поверхности объекта.

4 типа поверхностей:

1. Ортотропные поверхности отражают падающий свет равномерно (диффузно) по всем направлениям. Их называют диффузными (ламбертовскими). Эти поверхности доминируют среди естественных и искусственных объектов – пески, рыхлый снег, сухой асфальт, грунт. Отличительная особенность – независимость яркости от положения наблюдателя.

Рис. 13.2

2. Зеркальные поверхности отражают падающий свет преимущественно под углом, равным углу падения. К ним относятся чистые стеклянные поверхности, пластики, металлические поверхности, лед, камни сухие, поверхности водных бассейнов. Применительно к реальным объектам термин “зеркальная поверхность” указывает на направленный характер отражения падающего света, но не означает, что отражение происходит в полном соответствии с законами геометрической оптики. Для реальных зеркальных отражений угол отражения = углу падения (идеально-отражающие поверхности - зеркало). При этом падающий свет рассеивается в некотором телесном угле относительно направления max.

Рис. 13.3

3. Обратно отражающие поверхности отражают свет преимущественно к источнику. Их называют изрытыми, антизеркальными, световозвращающими. Такое отражение характерно для сельскохозяйственных культур, лугов и другой растительности.

Рис. 13.4

4. Смешенное отражение. Для таких поверхностей характерно наличие 2-х или 3-х типов отражения. В общем случае можно выделить диффузную, зеркальную и обратную составляющие, а индикатриса имеет 2 max. Такое отражение наблюдается у рисовых полей, лугов, покрытых расой и др. аналогичных объектов.

Рис. 13.5

С увеличением высоты шероховатостей зеркальная компонента уменьшается и отражение стремится к диффузному. Иногда диффузное отражение преобладает и для объектов с гладкими поверхностями (молочное стекло). В таком случае большая часть падающего света проникает в приповерхностный слой и рассеивается массой мелких неоднородностей (диффузное излучение из внутренних областей объекта).

Отражение диффузное

Отражение от объекта может быть диффузным и зеркальным. При диффузном отражении свет как бы проникает под поверхность объекта, поглощается и вновь испускается. Положение наблюдателя не имеет значения, т.к. диффузно отраженный свет рассеивается равномерно по всем направлениям. Зеркальное же отражение происходит от внешней поверхности объекта. При диффузном отражении поверхности имеют одинаковую яркость независимо от угла обзора.

Свет точечного источника отражается от поверхности по закону Ламберта:

- интенсивность отраженного света.

- интенсивность точечного источника.

- коэффициент диффузного отражения.

- угол между направлением света и нормалью к поверхности.

Рис. 13.6

Предметы, освещенные одним точечным источником света, выглядят контрастными (предмет в темной комнате при фотовспышке). Отсутствует рассеянный свет, как в реальной ситуации, когда на объекты падает еще и свет, отраженный от окружающей обстановки, например, от стен комнаты, других предметов.

Поэтому введем коэффициент рассеяния (const):

- интенсивность отраженного света;

- коэффициент диффузного отражения рассеянного света .

Если есть 2 объекта, одинаково ориентированные относительно источника, но расположенные на разном расстоянии, то их интенсивность ( ) по данной формуле будет одинакова. А ведь д.б. обратно пропорциональна расстоянию до объекта.

Тогда модель освещения примет вид:

- расстояние до объекта от точечного источника;

- произвольная const.

Если предполагается, что точка наблюдения находится в , то определяется положением объекта, ближайшего к точке наблюдения.

Для цветных поверхностей модель освещения применяется к каждому из 3-х основных цветов.

Зеркальное отражение

Что означает термин «идеальное зеркало»? Будем полагать, что у такого зеркала идеально ровная отполированная поверхность, поэтому одному отраженному лучу соответствует только один падающий луч. Зеркало может быть затемненным, то есть поглощать часть световой энергии, но все равно остается правило: один луч падает — один отражается. Можно рассматривать также «неидеальное зеркало». Это будет означать, что поверхность неровная. Один падающий луч порождает несколько отраженных лучей, образующих некоторый конус, возможно несимметричный, с осью вдоль линии падающего луча идеального зеркала. Конус соответствует некоторому закону распределения интенсивностей, простейший из которых описывается моделью Фонга — косинус угла, возведенный в некоторую степень.

Зеркальное отражение можно получить от любой блестящей поверхности. Осветим ярким светом яблоко – световой блик возникнет в результате зеркального отражения, а свет, отраженный от остальной части яблока – диффузный. В месте светового блика яблоко кажется не красным, а белым, т.е. окрашенным в цвет падающего света. Т.к. зеркально отраженный свет сфокусирован вдоль вектора отражения, блики при движении наблюдателя тоже смещаются.

Учитывать зеркальное отражение в модели освещения впервые предложил Фонг. Эти блики существенно увеличивают реалистичность изображения, ведь редкие реальные поверхности не отражают свет, поэтому эта составляющая очень важна. Особенно в движении, потому что по бликам сразу видно изменение положения камеры или самого объекта.

Зеркальное отражение света является направленным. Угол отражения от идеальной отражающей поверхности (зеркала) = углу падения; в любом другом положении наблюдатель не видит зеркально отраженный свет .

Рис. 13.7

Для неидеально отраженных поверхностей (яблоко) интенсивность отраженного света резко падает с увеличением . У гладких поверхностей распределение узкое, сфокусированное, у шероховатых – более широкое.

Эмпирическая модель Фонга:

- кривая отражения, представляет собой отношение зеркально отраженного света к падающему, как функцию угла падения и длины волны .

Большие значения n дают сфокусированные распределения характеристик металлов и др. блестящих поверхностей, а малые – более широкие распределения для малоблестящих поверхностей.

Рис. 13.8

Коэффициент отражения для металлов (n) может быть больше 80%, а для неметаллов – всего 4%.

Функция очень сложна, поэтому ее обычно заменяют коэффициентом 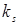, который выбирается из эстетических соображений, либо определяется экспериментально.

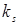обычно одинакова для всех 3-х основных цветов.

Модель освещения (функция закраски):

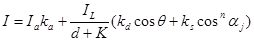
Если есть несколько (m) источников света, то их эффекты суммируются:

Пропускание света (прозрачность)

Поверхности могут направленно и диффузно пропускать свет. Направленное пропускание света происходит сквозь прозрачные вещества (стекло). Через них хорошо видны предметы, несмотря на то, что лучи света, как правило, преломляются, т.е. отклоняются от первоначального направления. Диффузное пропускание света происходит сквозь просвечивающиеся материалы (замерзшее стекло), в которых поверхностные неоднородности приводят к беспорядочному перемешиванию световых лучей. Поэтому очертания предмета, рассмотренного через такие материалы, размыты.

При переходе из одной среды в другую световой луч преломляется (торчащая из воды палка кажется согнутой). Преломление рассчитывается по закону Снеллиуса: падающий и преломляющий лучи лежат в одной плоскости, а углы падения и преломления определяются:

Рис. 13.9

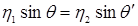
- показатели преломления двух сред.

Моделирование пропускания света осуществлялось несколькими способами. В простейшем из них преломление не учитывалось совсем и световые лучи пересекают поверхность без изменения направления. Т.о. все, что видимо на луче зрения при его прохождении через прозрачную поверхность, геометрически также принадлежит этому лучу. При наличии преломления геометрический и оптический лучи зрения не совпадают. Без учета преломления виден предмет В, с преломлением – А. На 1-ый взгляд достаточно знать угловые соотношения в точках пересечения луча с объектом. Но это не так, т.к. длина пути луча в объекте тоже меняется, 1) не совпадают т. выхода луча из объекта; 2) меняется количество поглощенного объектом света, поэтому исходящий луч имеет другую интенсивность.

Рис. 13.10

Простое пропускание света можно встроить в любой алгоритм удаления невидимых поверхностей, кроме z – буфера, т.к. поверхности в нем обрабатываются в произвольном порядке. Если используется алгоритм построчного сканирования и передний многоугольник оказывается прозрачным, определяется ближайший из др. многоугольников, внутри которых находится сканирующая строка. Уровень закраски определяется как взвешенная сумма уровней, вычисленных для каждого из двух многоугольников:

— интенсивность видимой поверхности,

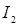— интенсивность поверхности за видимой,

— коэффициент прозрачности поверхности 1 ( 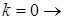полная прозрачность

полная непрозрачность).

Если 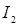тоже прозрачна, то алгоритм применяется рекуррентно, пока не встретится непрозрачная поверхность или фон.

При расчете общей интенсивности обычно используется направленный пропущенный свет, поскольку учет диффузного вызывает много сложностей. Поэтому моделируются только прозрачные вещества.

Общий вид модели освещения:

,

где а – рассеянный свет, d – диффузноотраженный свет, s - зеркальноотраженный свет, t – пропущенный свет.

Рис. 13.11

Специальные модели

Для исследования общих закономерностей отражения поверхностей сложной структуры используют специальные модели:

1) Модель Торрэнса-Спэрроу (фацентная модель).

Поверхность представляется в виде совокупности случайно ориентированных микроскопических зеркальных граней. Отражение от каждой микрограни определяется по формуле, затем методами геометрической оптики учитывается затенение микрограней соседними и маскирование части зеркально отраженного света соседними микрогранями. Эта модель позволяет в аналитической форме учесть длину волны и угол падения лучей.

2) Модель слоистая используется для растительности, покрытой листвой. Каждый слой образован отдельными, в общем случае не перекрывающимися площадками определенных форм и размеров и обладающими ортотропным отражением. Отражение определяется затенением отражающих площадок нижних слоев вышележащими. Получить аналитическое решение такой модели сложно, обычно используют метод Монте-Карло. Результаты моделирования показывают, что поверхности такой структуры обладают обратным отражением.

Модели, основанные на статистическом описании структуры отражающих поверхностей, сложны. Это очень ограничивает их применение в машинной графике. Обычно используют приближенные модели. Полагают, что форма индикатрисы отражения не зависит от длины волны.

1. Методы закраски полигональной сетки.

Существует 3 способа закраски объектов, заданных полигональными сетками:

Однотонная закраска

Вычисляется 1 уровень интенсивности, который используется для закраски всего многоугольника. При этом предполагается, что:

1) Источник света расположен в бесконечности ( 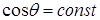на всей полигональной грани)

2) Наблюдатель находится в бесконечности ( на всей полигональной грани)

3) Многоугольник п.с. реальную моделируемую поверхность, а не является аппроксимацией криволинейной поверхности.

Если первое или второе условие неприемлемо, можно использовать усредненное значение , вычисленные в центре многоугольника.

Третье предположение тоже часто не выполняется, но оно оказывает большое влияние на результат: каждая из видимых граней аппроксимированной поверхности хорошо отличима от других, т.к. интенсивность каждой из этих граней отличается от интенсивности соседних граней (эффект полос Маха).

Интерполяция интенсивностей (метод Гуро)

Метод Гуро позволяет получать сглаженный объект на этапе визуализации, не внося изменения в геометрическую модель (полигональные сетки). Полосы Маха значительно уменьшаются.

Процесс закраски осуществляется в 4 этапа:

1) Вычисляются нормали к поверхностям.

2) Определяются нормали в вершинах путем усреднения нормалей по всем граням, которым принадлежит вершина.

Рис. 13.12

3) Используя нормали в вершинах и применяя произвольный метод закраски, вычисляются значения 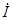в вершинах.

4) Каждый многоугольник закрашивается путем линейной интерполяции значений 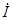в вершинах сначала вдоль каждого ребра, а затем между ребрами вдоль каждой сканирующей строки:

Рис. 13.13

Интерполяция вдоль ребер легко объединяется с алгоритмом удаления скрытых поверхностей, построенном на принципе построчного сканирования. Для всех ребер запоминается начальное 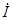, а также изменение 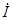при каждом единичном шаге по координате y. Заполнение видимого интервала на сканирующей строке производится путем интерполяции между значениями 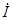на двух ребрах, ограничивающих интервал. Для цветных объектов отдельно интерполируется каждая из компонент цвета.

Интерполяция векторов нормали (метод Фонга)

Закраска Фонга требует больших вычислительных затрат, но она позволяет разрешить многие проблемы метода Гуро. При закраске Гуро вдоль сканирующей строки интерполируется значение , а при закраске Фонга – вектор нормали. Затем он используется в модели освещения для вычисления 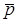. При этом достигается лучшая локальная аппроксимация кривизны поверхности, и получается более реалистичное изображение. Особенно правдоподобно выглядят зеркальные блики, которые в методе Гуро сильно размываются.

Этапы закраски:

1) Вычисляются нормали к поверхностям.

2) Определяются нормали в вершинах путем усреднения нормалей по всем граням, которым принадлежит вершина.

3) Для каждой точки сканирующей строки определяется вектор нормали путем линейной интерполяции значений N (сначала в вершинах, затем - между ребрами).

4) Для каждой точки сканирующей строки вычисляется значение интенсивности .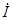

Метод Фонга приводит к более качественным результатам, т.к. аппроксимация нормали осуществляется в каждой точке. Полосы Маха практически исчезают.

1. Получение теней.

Изображение с построенными тенями выглядит гораздо реалистичнее, и, кроме того, тени очень важны для моделирования. Например, особо интересующий нас участок может оказаться невидимым из-за того, что он попадает в тень. А в строительстве, при разработке космических аппаратов тени влияют на расчет падающей солнечной энергии, обогрев и кондиционирование воздуха. Если положение наблюдателя и источника света совпадают, то теней не видно, но они появляются, когда наблюдатель перемещается в любую другую точку. Тень стоит из 2-ух частей: полутени и полной тени. Полная тень – центральная, темная, резко очерченная часть, а полутень – окружающая ее более светлая часть. Распределенные источники света создают как тень, так и полутень: в полной тени свет вообще отсутствует, а полутень освещается частью распределенного источника.

Точечные источники создают только полную тень. Из-за больших вычислительных затрат рассматривается только полная тень, образуемая точечным источником света.

Легче всего, когда источник находится в бесконечности, тогда тени определяются с помощью ортогонального проецирования. Если источник расположен на конечном расстоянии, то используется перспективная проекция.

Рассмотрим рисунок. В этом случае тени образуются двояко:

1) собственно тень на объекте;

2) проекционная тень.

Собственная тень получается тогда, когда сам объект препятствует попаданию света на некоторые его грани. Алгоритм затенения в этом случае идентичен алгоритму удаления скрытых поверхностей. В алгоритме удаления скрытых поверхностей определяются поверхности, которые можно увидеть из точки зрения, а в алгоритме затенения – поверхности, которые можно “увидеть” из источника света. Поверхности, видимые из источника света и из точки зрения, не лежат в тени. Поверхности, видимые из точки зрения, но невидимые из источника света, находятся в тени. Поэтому удобно использовать 1 алгоритм, последовательно применяя его к точке зрения и к каждому из точечных источников света.

Рис. 13.14

Если один объект препятствует попаданию света на другой, то получается проекционной тень (горизонтальная плоскость на рис.). Чтобы найти такие тени, надо построить проекции граней на сцену. Центр проекции – в источнике света. Т.о. находятся теневые многоугольники для всех граней и заносятся в структуру данных. Чтобы не вносить в нее слишком много многоугольников, можно проецировать контур каждого объекта, а не отдельные грани.

Для создания различных видов из разных точек зрения не надо вычислять тени заново, т.к. они зависят только от положения источника света и не зависят от положения наблюдателя.

Источник на бесконечности

Рис. 13.15

В случае бесконечно удаленного источника света мы предполагаем, что лучи света, приходящие к объекту, полностью параллельны. Это позволит нам решить уравнение проекции только раз и применять полученное решение ко всем вершинам объекта.

Общая постановка задачи:

Имея точку источника света и вершину объекта , мы хотим получить проекцию вершины объекта на плоскость z=o, т.е. точку тени .

Из подобных треугольников получаем:

(1.1)

Решая это уравнение относительно , получаем:

(1.2)

Если принять, что L это вектор из точки P к источнику света, то точку S можно выразить как:

(1.3)

Т.к. мы производим проекцию на плоскость z=0, то уравнение (1.3) можно переписать в следующем виде:

(1.4)

или

(1.5).

Решая (1.3) относительно и , получаем

(1.6)