Алгоритм Робертса 3 страница

или в матричной форме:

(1.7)

Теперь имея координаты точки P в мировом координатном пространстве, можно получить ее проекцию на плоскость z=0 просто путем умножения на матрицу

(1.8).

Локальный источник

Уравнение (1.6) для бесконечно удаленного источника света может быть обобщено для случая, когда источник света находится на конечном расстоянии от объекта. В этом случае нам понадобятся дополнительные вычисления на каждую вершину, т.к. каждая вершина имеет, в общем случае, свое собственное направление на источник света. Тем не менее, в этом случае мы тоже можем перенести большую часть вычислений в матрицу .

Если L это точка расположения источника света, то (1.3) принимает вид:

(1.9)

И снова нам необходимо произвести проекцию на плоскость z=0, тогда.

(1.11)

Если использовать гомогенизацию после преобразования, то (1.11) можно записать в виде матрицы:

(1.12).

Опять, имея координаты точки P в мировом координатном пространстве, можно записать:

(1.13)

После чего провести гомогенизацию точки S для получения проекции точки P на плоскость z=0.

1. Фактура. Нанесение узора на поверхность.

В машинной графике фактурой называется детализация строения поверхности. Существует 2 вида детализации:

1. Нанесение заданного узора на гладкую поверхность (регулярная и стохастическая текстуры).

2. Создание неровностей на поверхности.

Нанесение узора на поверхность. Регулярная текстура.

Характерные точки узора из пространства текстуры переносятся в объектное пространство, затем в пространство изображения и определенным образом соединяются отрезками. Главным при этом является отображение, поэтому задача сводится к преобразованию систем координат.

Пусть рисунок узора задан в прямоугольной системе координат (u,w), а поверхность – в другой прямоугольной системе координат (x,y), то для нанесения узора на поверхность надо найти или задать функцию отображения одного пространства на другое:

, или , .

Обычно предполагается, что функция отображения линейна:

после

где коэффициенты A, B, C, D выводятся из соотношения между двумя известными точками в системах координат.

Пример.

Узор на рис. а) надо отобразить на кусок поверхности, заданный десятой частью сферы.

Рис. 13.16

Параметрическое представление куска сферы:

Пусть функция отображения линейна и имеет вид:

, .

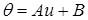Углы узора переходят в углы куска следующим образом:

, при , , при ,

, при , , при ,

Отсюда , , , .

Функция отображения: ,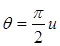

или обратное преобразование: , .

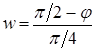В таблице приведено отображение одной линии узора из пространства (u-w) в пространство , а затем в декартовы координаты (x,y,z). Таблица 13.1

u	w			x	y	z
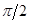
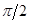
¼	¼ ½ ¾			0,38 0,38 0,35 0,32 0,27	0,92 0,90 0,85 0,77 0,65	0,20 0,38 0,56 0,71

Нанесение узора на поверхность. Стохастическая текстура.

Используется метод обратного трассирования лучей. Центр каждого 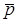изображения проецируется на поверхность объекта и по координатам т. на поверхности определяется соответствующая ей т. в пространстве фактурном. Далее используются процедуры сглаживания для устранения дискретизации.

Рассмотренный узор был задан математически, но он м.б. также нарисован от руки или получен путем сканирования фотографий. Для нанесения рис. на поверхность необходимо:

¾ отображение объектного пространства (ОП) в пространство изображения (ПИ);

¾ преобразование из фактурного пространства (ФП) в ОП.

Рассмотрим алгоритм разбиения Кэтмула:

1) Кусок поверхности разбивается на фрагменты до тех пор, пока фрагмент не будет покрывать центр только одного .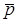

2) Производится отображение параметрических значений центра фрагмента или 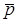в ФП.

3) Находится интенсивность 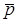по узору.

Пример. (Исходные данные те же)

Узор задан на растре .

Рис. 13.17

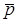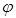Кусок поверхности разбиваем на фрагменты. Для того, чтобы фрагмент покрывал центр только одного , надо 4 разбиения. В ПИ этот фрагмент имеет прямоугольную форму. Пределы изменения и в ОП:

С помощью функции обратного отображения из ОП в ФП :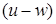

,

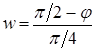
получим координаты углов фрагмента в ФП:

, ,

, ,

, ,

, ,

В ФП – это квадрат. На растре 64 64 часть1/16 соответствует 4 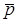. Интенсивность 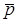в ПИ определяется путем усреднения интенсивностей 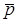в соответствующей части ФП. Кусок фрагмента 4 4 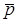содержит 7 черных 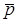, поэтому в ПИ интенсивность .

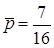Недостаток: такой метод поточечной выборки приводит к сильному лестничному эффекту.

1. Фактура. Создание неровностей на поверхности.

Рассматривая рисунок, единственный способ определить, что изображение отображает рельефную поверхность, — это проанализировать изменения яркости отдельных участков изображения. Наш мозг делает это автоматически, незаметно для нас. В результате мы четко определяем, что будет выпуклостью, что впадиной.

Рис. 13.18

Очень похоже на выдавливание (чеканку). Но, по сути, единственное, что было сделано для придания объемности плоскому изображению, — это правильное наложение ярких и темных участков. Остальное делает наш мозг.

Но как определить, какие биты изображения делать яркими, и наоборот. Очень просто. Большинство людей в течение своей жизни продолжительно находятся в условиях, когда свет исходит сверху. Таким образом, человек привык, что большинство поверхностей сверху ярко освещены, а снизу, наоборот, находятся в тени и будут темнее. Таким образом, если лаз воспринимает светлые и темные области на объекте, то человек воспринимает их как рельеф.

Рис. 13.19

Посмотрев на тот же рисунок, только развернутый на 180 градусов, можно заметить, что он стал похож на полную противоположность предыдущему. То, что раньше казалось выпуклым, стало вогнутым, и наоборот. А ведь это то же самое изображение. Тем не менее, наш мозг все же не настолько глуп. Если вы сможете заставить себя подумать, что свет исходит снизу, мозг воспроизведет информацию так же, как на первом изображении.

Для того, чтобы поверхность казалась шероховатой, можно оцифровать фотографию нерегулярной фактуры и отобразить ее на поверхность. Но при этом будет казаться, что неровности нарисованы на гладкой поверхности.

Рельефное текстурирование

Первый метод основан на использовании рельефных карт (Bump Mapping).

Рис. 13.20

Рельефная карта — это обычная текстура, только в отличие от первой, несущей информацию о цвете определенных участков, рельефная карта несет информацию о неровностях. Самый распространенный способ представить неровности - это применить карту высот. Карта высот — это текстура в оттенках серого, где яркость каждого пикселя представляет, насколько он выдается из базовой поверхности.

Используя карту высот, можно имитировать неровности практически любой поверхности: дерево, камень, шелушащуюся краску и т.д. Конечно, у всего есть свои пределы. Используя bump mapping, нельзя имитировать крупные впадины и возвышенности, но вот для имитации неровностей и шероховатостей на поверхности этот метод подходит идеально.

По сути, это логическое продолжение техники просчета по Фонгу, где интерполируется нормаль к поверхности по всему полигону, и этот вектор используется для дальнейшего определения яркости соответствующего пикселя. Реализуя его, немного меняется направление вектора нормали, основываясь на информации, содержащейся в карте высот. Изменяя положение вектора нормали в конкретной точке полигона, меняется яркость текущего пикселя (закон косинуса из теории света).

Рис. 13.21

Для того, чтобы этого достичь, существует несколько путей. Вначале необходимо преобразовать информацию о высоте неровностей на карте высот в информацию о величине подстройки вектора нормали. Для этого нужно преобразовать высоты с карты в маленькие векторы. Более светлые квадраты соответствуют более выпуклым участкам. После этого для каждого пикселя рассчитывается вектор, указывающей направление уклона поверхности. Рисунок 13.22 демонстрирует нам это. Маленькие векторы указывают на уменьшение высоты.

Рис. 13.22

Для определения этих векторов определяется величина градиента для каждого пикселя:

x_gradient = рixel(x-1, y) – pixel(x+1, y) y_gradient = pixel(x, y-1) - pixel(x, y+1),

Рис. 13.23

где x и y — координаты соответствующего пикселя.

Теперь, имея в руках значения градиентов, можно подкорректировать вектор нормали в соответствующем пикселе.

Рис. 13.24

На рис. 13.24 показан полигон с изначальным вектором нормали, обозначенным n. Также показаны два вектора, которые будут использованы для изменения положения (направления) нормали к пикселю под ним. Оба вектора должны располагаться параллельно осям координат применяемой карты высот.

На рисунке ??? показаны карта высот и полигон. На обоих рисунках показаны направления U и V осей координат карты (текстуры) высот.

Рис. 13.25

Пересчитать новый вектор нормали легко:

New_Normal = Normal + (U*x_gradient) + (V*y_gradient)

Получив новый вектор нормали, можно просчитать яркость данного пискеля, используя ранее изученную технологию затенения по Фонгу.

Для затенения по Фонгу применялся способ с заранее просчитанной картой, которая представляет собой набор яркостей для всех возможных нормалей на полигоне. Таким образом, быстро выполняемым вариантом рельефного текстурирования будет просчет смещений к карте затенения по Фонгу. Результирующей яркостью пикселя будет сумма значений, полученных с карты затенения и рельефной карты. Используя этот подход, мы одновременно будем производить затенение по Фонгу с учетом рельефности рисунка.

Метод возмущения нормали

В векторе нормали к настоящей шероховатой поверхности и, следовательно, в направлении отражения есть небольшая случайная составляющая. На этой основе Блинн разработал метод возмущения нормали (Normal Mapping) для построения неровных поверхностей. Строится новая поверхность, которая выглядит шероховатой, путем внесения в направление нормали функции возмущения P(x,y):

,

где Q - поверхность, - новая поверхность, n - нормаль в т. (x,y).

В качестве P(x,y) можно использовать почти любую функцию, у которой существуют частные производные. Если узор не определяется аналитически, то функция возмущения записывается как двумерная таблица цветов с индексами x и y. Промежуточные значения вычисляются билинейной интерполяцией табличных величин, а производные вычисляются методом конечных разностей.

В то время как бампмаппинг всего лишь изменяет существующую нормаль для точек поверхности, нормалмаппинг полностью заменяет нормали при помощи выборки их значений из специально подготовленной карты нормалей (normal map). Эти карты обычно являются текстурами с сохраненными в них заранее просчитанными значениями нормалей, представленными в виде компонент цвета RGB, в отличие от 8-битных черно-белых карт высот в бампмаппинге.

В общем, как и бампмаппинг, это тоже "дешевый" метод для добавления детализации к моделям сравнительно низкой геометрической сложности, без использования большего количества реальной геометрии, только более продвинутый. Одно из наиболее интересных применений техники - существенное увеличение детализации низкополигональных моделей при помощи карт нормалей, полученных обработкой такой же модели высокой геометрической сложности. Карты нормалей содержат более подробное описание поверхности, по сравнению с бампмаппингом и позволяют представить более сложные формы.

Рис. 13.26

Карты нормалей предоставляют более эффективный способ для хранения подробных данных о поверхностях, по сравнению с простым использованием большого количества полигонов. Единственное серьезное их ограничение в том, что они не очень хорошо подходят для крупных деталей, ведь нормалмаппинг на самом деле не добавляет полигонов и не изменяет форму объекта, он только создает видимость этого. Это всего лишь симуляция деталей, на основе расчета освещения на пиксельном уровне. На крайних полигонах объекта и больших углах наклона поверхности это очень хорошо заметно. Поэтому наиболее разумный способ применения нормалмаппинга состоит в том, чтобы сделать низкополигональную модель достаточно детализированной для того, чтобы сохранялась основная форма объекта, и использовать карты нормалей для добавления более мелких деталей.

Карты нормалей обычно создаются на основе двух версий модели, низко- и высокополигональной. Низкополигональная модель состоит из минимума геометрии, основных форм объекта, а высокополигональная содержит все необходимое для максимальной детализации. Затем, при помощи специальных утилит они сравниваются друг с другом, разница рассчитывается и сохраняется в текстуре, называемой картой нормалей. При ее создании дополнительно можно использовать и bump map для очень мелких деталей, которые даже в высокополигональной модели не смоделировать (поры кожи, другие мелкие углубления).

Карты нормалей изначально были представлены в виде обычных RGB текстур, где компоненты цвета R, G и B (от 0 до 1) интерпретируются как координаты X, Y и Z. Каждый тексель в карте нормалей представлен как нормаль точки поверхности.

Замечание1: Эффект шероховатости зависит от масштаба изображаемого объекта. Если размер объекта в увеличивается в 2 раза, то величина вектора нормали увеличивается в 4 раза, а его возмущения — только в 2 раза. Это приведет к тому, что увеличенный объект будет казаться более гладким. Но масштаб фактуры не зависит на перспективном изображении от перемещения объекта в пространстве по направлению к т. зрения или от нее.

Замечание 2: Может появиться лестничный эффект, но можно воспользоваться способом усреднения по площади фактуры или методами устранения лестничного эффекта, основанными на предварительной фильтрации, что приведет к сглаживанию фактуры. Надо рассчитывать изображение с разрешением, большим, чем у дисплея, а затем отфильтровать или усреднить его и вывести с более низким разрешением экрана.

Использование фрактальных поверхностей

Второй метод построения шероховатости основан на фрактальных поверхностях. Фрактальная поверхность состоит из случайно заданных полигональных поверхностей. С помощью этого метода изображаются природные объекты – камни, деревья, облака.

Для получения полигональной фрактальной поверхности исходный многоугольник рекурсивно разбивается на фрагменты (рис.). Для этого можно, например, случайным образом сместить центр и середины сторон многоугольника, причем и исходный и полученный многоугольники не обязательно д.б. плоскими.

Рис. 13.27

Одно из преимуществ фрактальных поверхностей в том, что их можно разбивать бесконечно и получить любой уровень детализации. Он может зависеть от положения наблюдателя: чем ближе точка зрения, тем с большей степенью детализации изображается поверхность. Затем фрактальная поверхность изображается с помощью любого подходящего алгоритма удаления невидимых поверхностей и любой модели освещения. Но число разбиений со скоростью выше линейной, поэтому между количеством разбиений и уровнем детализации д.б. некоторый компромисс. Иначе потребуется слишком много вычислений.

Использование карт смещения

Наложение карт смещения (Displacement Mapping) является методом добавления деталей к трехмерным объектам. В отличие от бампмаппинга, когда картами высот правильно моделируется только освещенность точки, но не изменяется ее положение в пространстве, что дает лишь иллюзию увеличения сложности поверхности, карты смещения позволяют получить настоящие сложные 3D объекты из вершин и полигонов. Этот метод изменяет положение вершин треугольников, сдвигая их по нормали на величину, исходя из значений в картах смещения. Карта смещения - это обычно черно-белая текстура, и значения в ней используются для определения высоты каждой точки поверхности объекта (значения могут храниться как 8-битные или 16-битные числа), схоже с bumpmap. Часто карты смещения используются (в этом случае они называются и картами высот) для создания земной поверхности с холмами и впадинами. Так как рельеф местности описывается двухмерной картой смещения, его относительно легко деформировать при необходимости, так как это потребует всего лишь модификации карты смещения и рендеринга на ее основе поверхности в следующем кадре.

Наглядно создание ландшафта при помощи наложения карт смещения представлено на картинке. Исходными были 4 вершины и 2 полигона, в итоге получился полноценный кусок ландшафта.

Рис. 13.27

Большим преимуществом наложения карт смещения является не просто возможность добавления деталей к поверхности, а практически полное создание объекта. Берется низкополигональный объект, разбивается на большее количество вершин и полигонов. Вершины, полученные в результате разбиения, затем смещаются по нормали, исходя из значения, прочитанного в карте смещения. Получается в итоге сложный 3D объект из простого:

Количество треугольников, должно быть достаточно большим для того, чтобы передать все детали, задаваемые картой смещений. Карты смещения лучше использовать совместно с бампмаппингом для создания мелких деталей, где достаточно правильного попиксельного освещения.

Наложение карт смещения можно по существу считать методом сжатия геометрии, использование карт смещения снижает объем памяти, требуемый для определенной детализации 3D модели. Громоздкие геометрические данные замещаются простыми двухмерными текстурами смещения, обычно 8-битными или 16-битными. Это снижает требования к объему памяти и пропускной способности. Другое преимущество в том, что применение карт смещения превращает сложные полигональные трехмерные сетки в несколько двухмерных текстур, которые проще поддаются обработке.

Но у карт смещения есть и некоторые ограничения, они не могут быть применены во всех ситуациях. Например, гладкие объекты, не содержащие большого количества тонких деталей, будут лучше представлены в виде стандартных полигональных сеток или иных поверхностей более высокого уровня, вроде кривых Безье. С другой стороны, очень сложные модели, такие как деревья или растения, также нелегко представить картами смещения. Есть также проблемы удобства их применения, это почти всегда требует специализированных утилит, ведь очень сложно напрямую создавать карты смещения (если речь не идет о простых объектах, вроде ландшафта). Многие проблемы и ограничения, присущие картам смещения, совпадают с таковыми у наложения карт нормалей, поскольку эти два метода по сути - два разных представления похожей идеи.

1. Фильтрация.

Фильтрация решает задачи определения цвета пикселя на базе имеющихся текселей из текстурного изображения.

Простейший метод наложения текстур называется поточечная выборка (single point-sampling). Суть его в том, что для каждого пикселя, составляющего полигон, выбирается один тексель из текстурного изображения, ближе всех расположенный к центру светового пятна. Совершается ошибка, так как цвет пикселя определяют несколько текселей, а выбран был только один.