Базові елементарні сигнали. Кількісний рахунок інформації.

Под элементарными колебаниями понимаются сигналы, математически описываемые функциями синус или косинус. На самом деле синус и косинус по сути один и тот же сигнал, только немного сдвинутый во времени.

Элементарные сигналы ( символы кода), составляющие кодовую комбинацию, должны различаться по какому-либо одному или нескольким параметрам, называемым часто кодовыми признаками. [2]

Элементарный сигнал может передавать дискретные сообщения типа крманд. Во многих промышленных устройствах ТУ - ТС передача одного видео - - или радиоимпульса означает передачу одной команды или одного сигнала телесигнализации. [3]

Сколько элементарных сигналов содержится в каждом информационном символе. [4]

Элементарным сигналом может служить пауза между импульсами или комбинации паузы и импульса и так далее. Эти сигналы должны различаться по какому-либо одному или нескольким параметрам, называемым часто кодовыми признаками. [5]

Элементарным сигналом может служить пауза между импульсами или комбинации паузы и импульса и так далее. [6]

К элементарным измерительным сигналам относятся постоянный во времени сигнал и сигналы, описываемые единичной и синусоидальной функциями, а также дельта-функцией.

Постоянный сигнал — самый простой из элементарных сигналов, описываемый математической моделью вида Y = А, где А — единственный параметр сигнала. Графики временной и частотной моделей постоянного сигнала приведены на рис. 10.4.

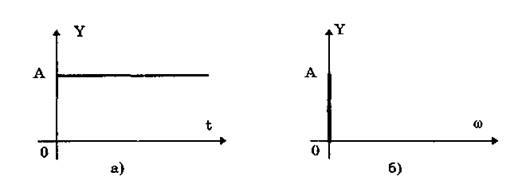
Рис. 10.4. Графики временной (а) и частотной (б) моделей

постоянного сигнала

Единичная функция, называемая иногда функцией Хевисайда, описывается уравнением

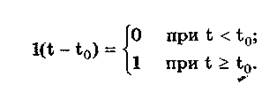
Она имеет один параметр — момент времени t₀. Ее временная и частотная модели представлены на рис. 10.5,а.

Дельта-функция описывается уравнением

Она также имеет один параметр — момент времени t₀. Графики временной и частотной моделей дельта-функции d(t) показаны на рис. 10.5, б. Из них видно, что дельта-функция имеет спектр бесконечной ширины.

Рис. 10.5. График моделей единичной (а) и дельта-функции(б)

Дельта-функция обладает следующим свойством:

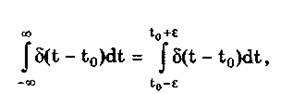
где e — любое, сколь угодно малое число. Она может рассматриваться как предельная функция однопараметрического семейства непрерывных функций, например нормального распределения с бесконечно малым СКО s:

Единичная и дельта-функции связаны между собой следующими выражениями:

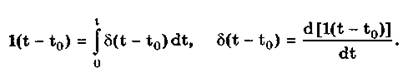
Важной особенностью дельта-функции является стробирующее действие, которое описывается уравнением

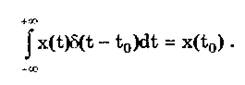
Оно используется для представления дискретизированной во времени функции с шагом дискретизации Dt:

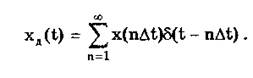
Гармонический сигнал описывается уравнением

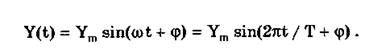(10.5)

Параметрами такого сигнала являются: амплитуда Y_m, период Т (или частота f=l/T, или круговая частота w) и начальная фаза j. График временной модели общеизвестен, а график частотной модели такого сигнала показан на рис. 10.6

.

Рис. 10.6. Спектр гармонического сигнала