Властивості

Якщо задані інтегровні функції 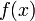, та 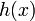та їхні відповідні перетворення Фур'є , та , тоді самому перетворенню властиво наступне:

Лінійність

Для довільних комплексних чисел a та b, якщо h(x) = aƒ(x) + bg(x), тоді  

Трансляція

Для довільного дійсного числа x₀, якщо h(x) = ƒ(x − x₀), тоді 

Модуляція

Для довільного дійсного числа ξ₀, якщо h(x) = e^2πixξ₀ƒ(x), тоді  .

Масштабування

Для не рівного нулю дійсного числа a, якщо h(x) = ƒ(ax), тоді  . Випадок a = −1 призводить до властивості "обернення часу", згідно з якою: якщо h(x) = ƒ(−x), тоді  .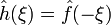

Спряження

Якщо , тоді 

Зокрема, якщо ƒ дійсне, тоді має місце "умова дійсності"  

Згортка

Якщо 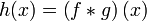, тоді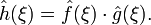 

Інформаційна эмність сигналу:

Ентропія являє собою логарифмічну міру безладдя стану джерела повідомлень і характеризує середній ступінь невизначеності стану цього джерела.

Ентропія Н визначається з формулою згідно з теоремою К. Шеннона, на основі якої, середня кількість інформації, що припадає на один символ, визначається

.

В інформаційних системах невизначеність знижується за рахунок прийнятої інформації, тому чисельно ентропія Н дорівнює кількості інформації І, тобто є кількісною мірою інформації.

У загальному випадку, відповідно до теорії ймовірностей, джерело інформації однозначно й повно характеризується ансамблем станів з імовірностями станів відповідно за умови, що сума ймовірностей всіх станів дорівнює 1.

Міра кількості інформації, як невизначеності вибору дискретним джерелом стану з ансамблю U, запропонована К. Шенноном в 1946 році й одержала назву ентропії дискретного джерела інформації або ентропії кінцевого ансамблю:

H(U) = - p_n log₂ p_n.

Ступінь невизначеності стану об'єкта (або так званого джерела інформації) залежить не тільки від числа його можливих станів, але й від імовірності цих станів. При нерівноймовірних станах варіанти вибору для джерела обмежуються.

Отже, основні властивості ентропії.

1. Ентропія є величиною дійсною й від’ємною, тому що значення ймовірностей p_n перебувають в інтервалі 0-1, значення завжди від’ємні, а значення 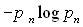відповідно додатні.

2. Ентропія – величина обмежена, тому що при 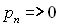значення також прямує до нуля, а при 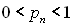обмеженість суми всіх доданків очевидна.

3. Ентропія дорівнює 0, якщо ймовірність одного зі станів джерела інформації дорівнює 1, і тим самим стан джерела повністю визначено (імовірності інших станів джерела дорівнюють нулю, тому що сума ймовірностей повинна бути 1).

4. Ентропія джерела із двома станами й при зміні співвідношення їхніх імовірносте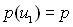й й визначається виразом

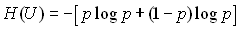
і досягає максимуму при рівності ймовірностей.

Так, якщо із двох можливих станів імовірність одного з них дорівнює 0,999 то ймовірність іншого стану відповідно дорівнює 1 – 0,999 = 0,001.

5. Ентропія об'єднаних статистично незалежних джерел інформації дорівнює сумі їх ентропій.

6. Ентропія максимальна при рівній імовірності всіх станів джерела інформації: .

В цьому окремому випадку кількісна міра Шеннона збігається з мірою Хартлі. Якщо повідомлення нерівноймовірні, то середня кількість інформації, що вміщується в одному повідомленні, буде меншою.

При використанні двійкової системи з рівними імовірностями виникнення «0» та «1», згідно із формулою Шеннона:

H = – 0,5 ⋅ log 2 0,5 – 0,5 ⋅ log 2 0,5 = 1.

Ентропія, а разом з нею і кількість інформації, дорівнюють нулю у випадках, коли p₁ = 0, або p₁ = 1.

Графік ентропії наведено на рисунку 2.1.

Рисунок 2.1 – Ентропія Н для двох можливих станів з імовірностями р1 та (1 – р1)

Для каналів передачі дискретних сигналів (дискретні каналу зв'язку) використають поняття технічної й інформаційної швидкості передачі даних.

Під технічною швидкістю передачі (англ. technical speed of transfer) розуміють число елементарних сигналів (символів), переданих по каналу за одиницю часу. Найпростіший елементарний символ – однополярний електричний імпульс тривалістю T. У дискретних каналах використовують, як правило, двополярні імпульси, позитивні на першій половині інтервалу Т і негативні на другій половині. Це дозволяє підтримувати нульовий потенціал кабелю й виконувати тактову синхронізацію прийому-передачі сигналів. Одиницею міри технічної швидкості V_t=1/T служить БОД – один символ у секунду. Смуга пропускання каналу зв'язку обмежується граничною частотою F_гр за рівнем загасання сигналу до рівня статистичних перешкод, при цьому значення технічної швидкості передачі даних не може бути вище F_гр без спеціальних пристроїв виділення інформаційних сигналів.

При відомій технічній швидкості Vt швидкість передачі інформації вимірюється в бітах у секунду й задається співвідношенням:

де H(s) – ентропія символу.

Для двійкових дискретних символів [0, 1] при постійній амплітуді імпульсів значення H(s) дорівнює 1. При числі L можливих рівноймовірних рівнів амплітуди імпульсів (рівень завад менший різниці рівнів амплітуд імпульсів) значення H(s) дорівнює log L.

Інформаційна ємність сигналу або повна кількість інформації в сигналі S (повідомленні, кодовій послідовності/слові) визначається повною кількістю N = t/T ентропії символів у бітах на інтервалі задання сигналу t:

.

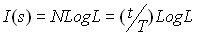Збільшення числа рівнів L збільшує пропускну здатність каналів зв'язку, але ускладнює апаратуру кодування даних і знижує завадостійкість.

Для неперервних сигналів передача по каналах зв'язку можлива тільки за умови, що максимальна інформаційна частота в сигналі F_max не перевищує граничної частоти F_гр передачі сигналів каналом зв'язку. Для оцінки інформаційної ємності безперервного сигналу виконаємо його дискретизацію з інтервалом t = 1/2F_max. Як установлено Котельниковим і Шенноном, за миттєвими відліками неперервного сигналу з таким інтервалом дискретизації аналоговий сигнал може бути відновлений без втрати інформації.

При повній тривалості сигналу 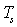число відліків:

.

Визначимо максимально можливе число вибірок у кожному відліку при наявності шуму в каналі із середньою потужністю Р_ш =2. При середній потужності сигналу P_s=s²:

L = = .

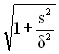Інформаційна ємність сигналу:

.

Інформаційні можливості сигналу зростають із розширенням його спектра й перевищенням його рівня над рівнем завад.