СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ

Переход от спектрального представления периодического сигнала к непериодическому можно осуществить, рассматривая соотношения комплексной формы ряда Фурье для сигналов с периодом T при T ® ¥. Из выражения (11.4) и рассмотренного примера следует, что при таком предельном переходе интервалы между соседними частотами дискретного спектра Dw = w_k – w_k–1 = 2p/T неограниченно уменьшаются, что приводит к непрерывному спектру, соответствующему непериодическому сигналу. Однако его коэффициенты Фурье F(jw_k) и амплитуды отдельных гармоник становятся бесконечно малыми. Поэтому при выполнении предельного перехода в выражении (11.4) будем оперировать не с коэффициентами F(jw_k), а выразим обе формулы (11.3) и (11.4) через произведение TF(jw_k) = F_T(jw_k), сохраняющее конечное значение при T ® ¥. Выполняя такую замену и учитывая связь между T и Dw, перепишем для комплексной формы:

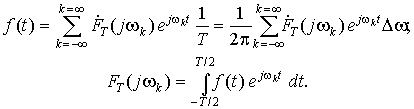
При предельном переходе при T ® ¥ Dw заменим на бесконечно малую dw, а дискретные значения частоты w_k — на непрерывные w, изменяющиеся в пределах от – до + . В результате сумма в выражении для f(t) перейдет в интеграл. Заменяя обозначение F_T(jw_k) на F(jw), окончательно получим для спектрального представления непериодического сигнала:

(11.5)

(11.6)

Полученные формулы определяют прямое (11.5) и обратное (11.6) интегральные преобразования Фурье. С их помощью непериодическая функция времени f(t) представляется совокупностью бесконечно большого числа синусоидальных составляющих с бесконечно малыми амплитудами dA(w) = 2(1/2p)|F(jw)| dw, частоты которых принимают любые значения от 0 до ¥. Величина F(jw), характеризующая распределение отдельных составляющих в спектре сигнала, называется спектральной плотностью. Напомним, что для сходимости несобственного интеграла (11.5) необходимо, чтобы функция f(t) была абсолютно интегрируемой, т. е. чтобы существовал интеграл . Это существенно ограничивает класс сигналов, допускающих преобразование Фурье в строгом математическом смысле: исключаются, в частности, все сигналы, не убывающие при t ® ± ¥.

Графическое изображение сплошного спектра непериодического сигнала включает частотные зависимости модуля F(w) = |F(jw)| и аргумента аrg F(jw) или вещественной и мнимой частей спектральной плотности F(jw) = F_в(w) + jF_м(w). Для абсолютно интегрируемых сигналов эти зависимости представляются ограниченными кривыми.

Определим спектр одиночного прямоугольного сигнала длительностью T (рис. 11.5, а). Поскольку f(t) отлична от нуля лишь в интервале времени –T/2 < t < T/2, пределы интегрирования в интеграле для спектральной плотности можно принять ограниченными:

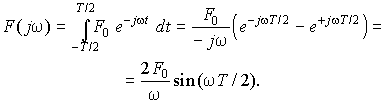
В рассматриваемом примере спектральная плотность F(jw) вещественна, так как исходный сигнал f(t) является четной функцией времени. График модуля |F(jw)| изображен на рис. 11.5, б. Он представляет непрерывную кривую и является неограниченным по частоте. С ростом частоты плотность амплитуды гармоник убывает.

Интеграл Фурье

Достаточные условия представимости функции в интеграл Фурье.

Для того, чтобы f(x) была представлена интегралом Фурье во всех точках непрерывности и правильных точках разрыва, достаточно:

1) абсолютной интегрируемости на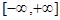

(т.е. интеграл сходится)

2) на любом конечном отрезке [-L, L] функция была бы кусочно-гладкой

3) в точках разрыва функции, ее интеграл Фурье определяется полусуммой левого и правого пределов в этих точках, а в точках непрерывности к самой функции f(x)

Интегралом Фурье функции f(x) называется интеграл вида:

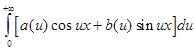
, где ,

.

Интеграл Фурье для четной и нечетной функции

Пусть f(x)-четная функция, удовлетворяющая условиям представимости интегралом Фурье.

Учитывая, что , а также свойство интегралов по симметричному относительно точки x=0 интервалу от четных функций, из равенства (2) получаем:

(3)

Таким образом, интеграл Фурье четной функции f(x) запишется так:

,

где a(u) определяется равенством (3).

Рассуждая аналогично, получим, для нечетной функции f(x) :

(4)

и, следовательно, интеграл Фурье нечетной функции имеет вид:

,

где b(u) определяется равенством (4).

Комплексная форма интеграла Фурье

, (5)

где

.

Выражение в форме (5) является комплексной формой интеграла Фурье для функции f(x).

Если в формуле (5) заменить c(u) его выражением, то получим:

, где правая часть формулы называется двойным интегралом

Фуpье в комплексной форме. Переход от интеграла Фурье в комплексной форме к интегралу

в действительной форме и обратно осуществим с помощью формул:

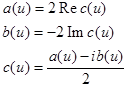
Формулы дискретного преобразования Фурье

Обратное преобразование Фурье.

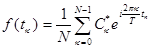
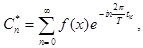
где n=1,2,... , k=1,2,...

Дискретным преобразованием Фурье - называется N-мерный вектор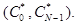

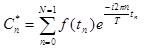
при этом, .