Кореляційний аналіз

Кореляційний аналіз – це статистичне дослідження (стохастичної) залежності між випадковими величинами (англ. correlation – взаємозв’язок). У найпростішому випадку досліджують дві вибірки (набори даних), у загальному – багатовимірні комплекси (групи) геологічних параметрів або об’єктів.

Мета кореляційного аналізу – забезпечити отримання деякої інформації про одну змінну за допомогою іншої змінної. В випадках, коли можливе досягнення мети, говорять, що змінні корелюють. В загальному вигляді сприйняття гіпотези про наявність кореляції означає, що зміна значення змінної А відбудеться одночасно з пропорційною зміною значення В.

Мірою залежності між експериментальними наборами даних є числа – коефіцієнти зв’язку.

Головні завдання кореляційного аналізу:

1) оцінка за вибірковими даними коефіцієнтів кореляції;

2) перевірка значущості вибіркових коефіцієнтів кореляції або кореляційного відношення;

3) оцінка близькості виявленого зв’язку до лінійного;

4) побудова довірчого інтервалу для коефіцієнтів кореляції.

Визначення сили та напрямку взаємозв’язку між змінними є однією з важливих проблем аналізу даних. В загальному випадку для цього застосовують поняття кореляції.

Коефіцієнт кореляції, а в загальному випадку кореляційна функція, дозволяють встановити степінь взаємозв’язку між змінними. Кореляція може бути лінійною або нелінійною в залежності від типу залежності, яка фактично існує між змінними. Досить часто на практиці розглядають тільки лінійну кореляцію (взаємозв’язок), але більш глибокий аналіз потребує використання для дослідження процесів нелінійних залежностей. Складну нелінійну залежність можна спростити, але знати про її існування необхідно для того, щоб побудувати адекватну модель процесу.

Кореляція відображає лише лінійну залежність величин, але не відображає їх функціональної зв'язаності. Наприклад, якщо обчислити коефіцієнт кореляції між величинами A = sin(x) та B = cos(x), він буде наближений до нуля, тобто залежність між величинами відсутня. Між тим, величини А та В очевидно зв'язані між собою за законом sin²(x) + cos²(x) = 1.

Використання можливе у випадку наявності достатньої кількості випадків для вивчення: для конкретного типу коефіцієнту кореляції складає від 25 до 100 пар спостережень.

Кореляція не означає причинність.

Дисректні та непреривні випалкові сигнали. Розложення періодичних сигналів у ряд Фур’є. Спектральна плотність не періодичних сигналів. Інтеграл Фур’є. Енергетичний спектр випадкових сигналів. Властивість перетворення Фур’є. Інформаційна ємність сигналів.

За формою сигнали поділяються на неперервні та дискретні.

Неперервні сигнали можуть приймати неперервну множину значень (континуум) в певному інтервалі (в часі і за рівнем).

Дискретні сигнали описуються за допомогою кінцевого набору чисел або дискретних значень певної функції.

Тобто, неперервні сигнали (рис. 3.15, а) зображуються функцією, безперервною в часі на відрізку спостереження 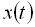, а дискретні (рис. 3.15, б) поступають тільки в певні моменти часу та зображаються дискретною функцією .

Рисунок 3.15 – Неперервні та дискретні сигнали

До елементарних детермінованих сигналів належить зокрема і одинична функція (стрибок).

При вивченні властивостей каналів передачі інформації, сигналів та завад абстрагуються від їх конкретної фізичної природи та призначення і оперують з їх моделями. Модель (англ. model) – це є вибраний спосіб опису об’єкта, процесу або явища, який відображає суттєві з погляду розв’язання даної задачі фактори. Оцінка електронних систем потребує виявлення кількісних співвідношень між основними параметрами джерела інформації і системи, тому дослідження здійснюється на математичних моделях.

Як відомо, інформація міститься в повідомленнях, зміст яких наперед невідомий і джерело інформації видає їх з певною ймовірністю. Передбачити точно зміну інформаційного параметра неможливо. Це означає, що інформаційний сигнал принципово являє собою випадкове коливання і його аналітичною моделлю може бути лише випадковий процес, який визначається імовірнісними характеристиками. Детерміноване коливання (сигнал) відображає відоме повідомлення, і немає сенсу його передавати. Йому відповідає модель у вигляді функції, що повністю визначена в часі. Разом з тим, вивчення моделей детермінованих сигналів дозволяє робити аналіз більш складних випадкових сигналів.

Сукупність детермінованих сигналів може подавати випадковий процес.

Периодическим сигналом (током или напряжением) называют такой вид воздействия, когда форма сигнала повторяется через некоторый интервал времени T, который называется периодом. Простейшей формой периодического сигнала является гармонический сигнал или синусоида, которая характеризуется амплитудой, периодом и начальной фазой. Все остальные сигналы будут негармоническими или несинусоидальными. Можно показать, и практика это доказывает, что, если входной сигнал источника питания является периодическим, то и все остальные токи и напряжения в каждой ветви (выходные сигналы) также будут периодическими. При этом формы сигналов в разных ветвях будут отличаться друг от друга.

Существует общая методика исследования периодических негармонических сигналов (входных воздействий и их реакций) в электрической цепи, которая основана на разложении сигналов в ряд Фурье. Данная методика состоит в том, что всегда можно подобрать ряд гармонических (т.е. синусоидальных) сигналов с такими амплитудами, частотами и начальными фазами, алгебраическая сумма ординат которых в любой момент времени равна ординате исследуемого несинусоидального сигнала. Так, например, напряжение u на рис. 2.1. можно заменить суммой напряжений и 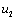, поскольку в любой момент времени имеет место тождественное равенство: . Каждое из слагаемых представляет собой синусоиду, частота колебания которой связана с периодом T целочисленными соотношениями.

Для рассматриваемого примера имеем период первой гармоники совпадающим с периодом негармонического сигнала T₁=T, а период второй гармоники в два раза меньшим T₂=T/2, т.е. мгновенные значения гармоник должны быть записаны в виде:

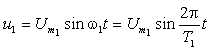
Здесь амплитуды колебаний гармоник равны между собой ( ), а начальные фазы равны нулю.

Рис. 2.1. Пример сложения первой и второй гармоники

негармонического сигнала

В электротехнике гармоническая составляющая, период которой равен периоду негармонического сигнала, называется первой или основной гармоникой сигнала. Все остальные составляющие называются высшими гармоническими составляющими. Гармоника, частота которой в k раз больше первой гармоники (а период, соответственно, в k раз меньше), называется

k - ой гармоникой. Выделяют также среднее значение функции за период, которое называют нулевой гармоникой. В общем случае ряд Фурье записывают в виде суммы бесконечного числа гармонических составляющих разных частот:

(2.1)

где k - номер гармоники; - угловая частота k - ой гармоники;

ω₁=ω=2π/T- угловая частота первой гармоники; - нулевая гармоника.

Для сигналов часто встречающихся форм разложение в ряд Фурье можно найти в специальной литературе. В таблице 2 приведены разложения для восьми форм периодических сигналов. Следует отметить, что приведенные в таблице 2 разложения будут иметь место, если начало системы координат выбраны так, как это указано на рисунках слева; при изменении начала отсчета времени t будут изменяться начальные фазы гармоник, амплитуды гармоник при этом останутся такими же. В зависимости от типа исследуемого сигнала под V следует понимать либо величину, измеряемую в вольтах, если это сигнал напряжения, либо величину, измеряемую в амперах, если это сигнал тока.

Разложение в ряд Фурье периодических функций

Таблица 2

График f(t)	Ряд Фурье функции f(t)	Примечание
		k=1,3,5,...
		k=1,3,5,...
		k=1,3,5,...
		k=1,2,3,4,5
		k=1,3,5,...
		k=1,2,3,4,5
		S=1,2,3,4,..
		k=1,2,4,6,..

Сигналы 7 и 8 формируются из синусоиды посредством схем, использующих вентильные элементы.

Совокупность гармонических составляющих, образующих сигнал несинусоидальной формы, называется спектром этого негармонического сигнала. Из этого набора гармоник выделяют и различают амплитудный и фазовый спектр. Амплитудным спектром называют набор амплитуд всех гармоник, который обычно представляют диаграммой в виде набора вертикальных линий, длины которых пропорциональны (в выбранном масштабе) амплитудным значениям гармонических составляющих, а место на горизонтальной оси определяется частотой (номером гармоники) данной составляющей. Аналогично рассматривают фазовые спектры как совокупность начальных фаз всех гармоник; их также изображают в масштабе в виде набора вертикальных линий.

Следует заметить, что начальные фазы в электротехнике принято измерять в пределах от –180⁰ до +180⁰ . Спектры, состоящие из отдельных линий, называют линейчатыми или дискретными. Спектральные линии находятся на расстоянии f друг от друга, где f - частотный интервал, равный частоте первой гармоники f .Таким образом, дискретные спектры периодических сигналов имеют спектральные составляющие с кратными частотами - f, 2f, 3f, 4f, 5f и т.д.