Оптимальная линейная фильтрация.

Пусть фильтр имеет линейную фазочастотную характеристику φ(ω)=-ωt₀, тогда спектральная плотность помехи равна:

S_п(ω)_в=S_п(ω)|К(jω)|²,
где К(jω) – комплексная частотная характеристика искомого фильтра.

Измерительный сигнал подвергается линейному преобразованию L, а сигнал погрешности после преобразований имеет вид: ε(t)=L[y(t)-y(t-t₀)]².

Преобразование Фурье этого сигнала: F_ε[ω]=S_c(jω)e^-jωt₀[K(jω)-1] (1)

Энергетический спектр погрешности: S_ε(ω)=S_пK(ω)²+S_c(ω)[K(ω)-1]² (2)

Найдём минимальное значение S_ε(ω) из dS_c(ω)/dK(ω)=0=2K(ω)S_п(ω)-2[1-K(ω)]S_c(ω) (3).

Откуда К_опт=S_c(ω)/S_c(ω)+S_п(ω) (4).

Реальный фильтр имеет характеристику вида: К_опт(jω)=S_c(ω)/S_c(ω)+S_п(ω)e^-jωt.

Подставив (4) в (2) получим формулу для определения минимальных значений фильтрации:

Выбор оптимальных параметров фильтра.

Пусть в СИ действует смесь полезного сигнала и помехи со спектральными плотностями S_c(ω), S_п(ω). Сигнал и помеха стационарно не коррелированы. Полезный сигнал менее широкополосен и его спектральная плотность снижается с ростом частоты. В этом случае существует некоторое оптимальное значение полосы пропускания частоты фильтра ω₀ (ФНЧ), минимизирующие значение СКО погрешности от действия помех СИ. В качестве фильтра можно использовать один из преобразователей СИ. Определим ω₀. Для этого найдём СКО погрешности от искажения измерительного сигнала при прохождении его через фильтр (σ[Δ_п]) и погрешности из-за прохождения части помехи через этот фильтр (σ[Δ_с]).

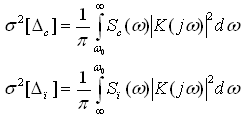
Суммарную погрешность фильтрации определим из соотношения σ²[Δ_∑]=σ²[Δ_п]+σ²[Δ_с]. Решив уравнение вида: dσ²[Δ_∑]/dω₀=0 можно найти ω₀. Если частотная характеристика средства измерения или фильтра нижних частот близка по виду к частотной характеристики идеального фильтра, то решение упрощается.

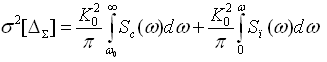
где К₀ – номинальный передаточный коэффициент СИ.