Дискриминантный анализ. Математическая модель.

Дискриминантный анализ является разделом многомерного статистического анализа, который позволяет изучать различия между двумя и более группами объектов по нескольким переменным одновременно. Дискриминантный анализ — это общий термин, относящийся к нескольким тесно связанным статистическим процедурам. Эти процедуры можно разделить на методы интерпретации межгрупповых различий — дискриминации и методы классификации наблюдений по группам.

Методы классификации связаны с получением одной или нескольких функций, обеспечивающих возможность отнесения данного объекта к одной из групп. Эти функции называются классифицирующими и зависят от значений переменных таким образом, что появляется возможность отнести каждый объект к одной из групп.

Задачи дискриминантного анализа можно разделить на три типа.

Задачи первого типа часто встречаются в медицинской практике. Медик может регистрировать различные переменные, относящиеся к состоянию больного, чтобы выяснить, какие переменные лучше показывают, что пациент, вероятно, выздоровел полностью, частично или совсем не выздоровел.

Второй тип задачи относится к ситуации, когда признаки принадлежности объекта к той или иной группе потеряны, и их нужно восстановить. (Пример: определение пола умершего человека по его останкам).

Задачи третьего типа связаны с предсказанием будущих событий на основании имеющихся данных (например прогноз выживаемости оперированных больных).

Дискриминация

Основной целью дискриминации является нахождение такой линейной комбинации переменных (в дальнейшем эти переменные будем называть дискриминантными переменными), которая бы оптимально разделила рассматриваемые группы. Линейная функция

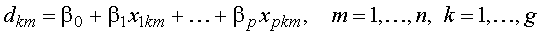(1)

называется канонической дискриминантной функцией с неизвестными коэффициентами 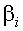. Здесь 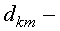значение дискриминантной функции для m–го объекта в группе k; 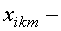значение дискриминантной переменной 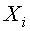для m–го объекта в группе k. С геометрической точки зрения дискриминантные функции определяют гиперповерхности в p-мерном пространстве. В частном случае при p=2 она является прямой, а при p=3 — плоскостью.

Введем следующие обозначения:

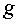 — число классов;

число дискриминантных переменных;

 — число наблюдений в k–й группе;

 — общее число наблюдений по всем группам;

В модели дискриминации должны соблюдаться следующие условия:

1. число групп: ;
2. число объектов в каждой группе: ;
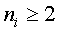3. число дискриминантных переменных: ;
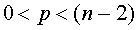4. дискриминантные переменные измеряются в интервальной шкале;
5. дискриминантные переменные линейно независимы;
6. ковариационные матрицы групп примерно равны;
7. дискриминантные переменные в каждой группе подчиняются многомерному нормальному закону распределения.