Симплекс- метод решения задачи линейного программирования. Симплекс- таблицы.

Симплекс метод разрабатывался применительно к задачам линейного программирования, в которых множество решений D представляло собой симплекс в пространстве Rⁿ т.е. D={x=Rⁿ| , }, где

n- мерным симплексом S_n называется выпуклая оболочка n- точек (x₁,x₂,x₃,…,x_n) не лежащих на одной (n-2) мерной плоскости.

Симплекс- это n- мерный выпуклый многогранник имеющий в точности n- вершин.

Решение соответствующей исходной точки называется начальным решением.

Базисом матрицы А называется набор m линейно независимых столбцов.

А матрица размерности (mxn)

Алгоритм симплекс- метода:

Для решения данной задачи необходимо выполнить следующие шаги:

Шаг 1: Инициализация

Разложим по исходному базису B={A_j1, A_j2,…., A_jm} небазисные вектор- столбцы матрицы А, т.е. найти координаты x_j=B^-1 b, вектор- столбцов А_i в базисе В. Разложение базисных вектор- столбцов известны x_ij=E_j. Также известны значения базисных переменных соответствующие базису В.

Шаг 2. Условия оптимальности.

Для каждого j от 1 до n вычислить симплекс- разность.

Если все симплекс- разности больше 0, то процесс решения задачи окончен и решение оптимальное, иначе перейти к шагу 3.

Шаг 3. Условие отсутствия решения задачи.

Выяснить существует ли хотя бы одна симплекс разность меньше 0.в этом случае процесс решения задачи окончен. Целевая функция задачи не ограничена. Если существует, то перейти к шагу 4.

Шаг 4: Итерация

Выбрать симплекс разность меньше 0 и с условием .

Соответствующие вектор столбцу x_j небазисная переменная х вводится в базис. Вычислить отношение для всех i для которых х_it>0 и найти минимальное из этих отношений.

Соответствующие k-ой строке матрицы А текущая базисная переменная выводится из базиса, при этом t- ая вводится в базис переменная принимает значение

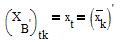и выполняется шаг 2.

Симплекс- таблица

Процесс нахождения экстремума с помощью симплекс-метода оформляется в виде специальных симплекс-таблиц. Симплекс-таблица составляется для каждой итерации по определенным правилам, что облегчает перебор базисных решений и позволяет избежать случайных ошибок.

симплекс-таблица представляет собой расширенную матрицу системы ограничений с некоторыми дополнительными столбцами и строками.

Симплекс- таблица размерности (m+1)*(n+2)

m- количество базисных переменных;

n- количество всех переменных.

M=

YB<m+1>	CB<m+1>
-	-

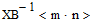
Построение симплекс-таблицы для задачи ЛП вида:

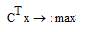
базисные переменные

( )- решение является допустимым и базисным, а исходная базисная матрица является единичной.

Начальное заполнение таблиц будет иметь вид:

YB	CB		X1	X2	….	Xn	Xn+1	Xm+n
n+1		b1	a11	a12
n+2		b2	a21	a22
…..	…..	….	…..	…..		…..	…..	…..
n+m		bm	am1	am2
					…..

Столбец таблицы который вводится в базис называется ведущим столбцом.

Строка таблицы соответствующая вектору выводимому из базиса называется ведущей строкой.

Элемент стоящий на пересечении ведущей строки и ведущего столбца называется ведущим элементом.

Пересчет симплекс- таблицы по закону:

Элемент ведущей строки делим на ведущие элементы.

Все элементы в ведущем столбце ,кроме ведущего заменяем не 0.

Заменяем номер ведущей строки на номер ведущего столбца.

Если в предыдущей таблице есть отрицательная симплекс- разность, то решение не является оптимальным, необходимо пересчитать таблицу еще раз.

2. Геометрическая интерпретация решения задачи линейного программирования.

Определение. Непустое множество планов общей (ос­новной) задачи линейного программирования называется многогранником решений.

Свойство. Если основная задача линейного программи­рования имеет оптимальный план, то максимальное значение целевая функция принимает в одной из вершин многогран­ника решений.

Вершину многогранника решений, в которой целевая фун­кция принимает максимальное значение, найти не сложно, если задача содержит не более двух переменных (в обшем случае задача, записанная в основной форме, содержит не более двух свободных переменных, то есть п-r < 2, где п -число переменных, r— ранг матрицы, составленной из ко­эффициентов в системе ограничений задачи).

Найдем решение задачи, состоящей в определении мак­симального значения функции

F = c₁x₁+c₂x₂ (*)

при условиях

(1)

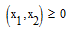(2)

Каждое из неравенств (1), (2) геометрически опреде­ляет полуплоскость соответственно с граничными прямыми a_i1x₁ + a_i2x₂ =b_i , i = 1,...k, x₁ = 0, х₂ = 0. Областью решений системы является множество точек, принадлежащих всем полуплоскостям, называемое в двумерном случае много­угольником решений.

Исходная задача линейного программирования состоит в нахождении вершины многоугольника решений, в которой целевая функция (*) принимает максимальное значение. Такая вершина существует тогда, когда многоугольник ре­шений не пуст и на нем целевая функция ограничена сверху. Для определения этой вершины построим линию уровня с₁х₁ + с₂х₂ = h, проходящую через многоугольник решений, и будем перемещать ее в направлении вектора С = (c₁c₂), орто­гонального ей, до тех пор пока она не пройдет через послед­нюю общую точку с многоугольником решений. Координаты этой точки и определяют оптимальный план задачи.

Отметим, что нахождение минимального значения линейной функции при данной системе ограничений отличается от нахож­дения ее максимального значения при тех же ограничениях лишь тем, что линия уровня с₁х₂ + c₂x₂ = h перемещается не в направ­лении вектора С = (с₁, с₂), а в противоположном направлении.