
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Двойственные задачи линейного программирования. Теоремы двойственности
Важную роль в линейном программировании имеет понятие двойственности. Рассмотрим две задачи линеного программирования
max{F(x) = CT x| Ax≤B, xi≥0, i =1,n} (1)
и
min{F(y) = BT y| AT y≥C, yj ≥0, j = 1,m}. (2)
Задачу (1) называют прямой, а связанную с ней задачу (2) – двойственной. Вместе они образуют симметрическую пару двойственных задач. Число переменных двойственной задачи равно количеству ограничений прямой. Кроме того, при переходе от прямой задачи к двойственной вектора B и C меняют местами, матрица A коэффициентов системы ограничений прямой задачи транспонируется, а знак неравенств в ограничениях меняют на противоположный. Смысл экстремума F(x) противоположен смыслу экстремума F(y) . Связь между задачами (1) и (2) взаимна, т.е. если прямой считать задачу (2), то в качестве двойственной ей будет соответствовать задача (1). Возможность перехода от прямой задачи к двойственной (и наоборот) устанавливается теоремой двойственности: если одна из задач (1) или (2) имеет оптимальное решение, то и другая также имеет оптимальное решение, причем оптимальные значения функции цели прямой и двойственной задач совпадают, т.е. max F(x) = min F( y) .
Если среди ограничений прямой задачи имеются равенства или на некоторые переменные не наложено условие неотрицательности, то построив двойственную ей задачу, получим пару несимметричных двойственных задач:

При этом выполняются следующие правила:
1. Если на переменную xi прямой задачи наложено условие неотрицательности, то i-е условие системы ограничений двойственной задачи является неравенством и наоборот.
2. Если на переменную xi прямой задачи не наложено условие неотрицательности, то i-е ограничение двойственной задачи записывается в виде строгого равенства.
3. Если в прямой задаче имеются ограничения равенства, то на соответствующие переменные двойственной задачи не накладывается условие неотрицательности.
Первая теорема двойственности. Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой, т.е.  .
.
Если целевая функция одной из пары двойственных задач не ограничена (для исходной задачи сверху, для двойственной снизу), то другая задача вообще не имеет планов.
^ Вторая теорема двойственности. План  исходной задачи и план
исходной задачи и план  двойственной задачи, являются оптимальными планами этих задач тогда и только тогда, когда для любого
двойственной задачи, являются оптимальными планами этих задач тогда и только тогда, когда для любого  выполняется равенство
выполняется равенство
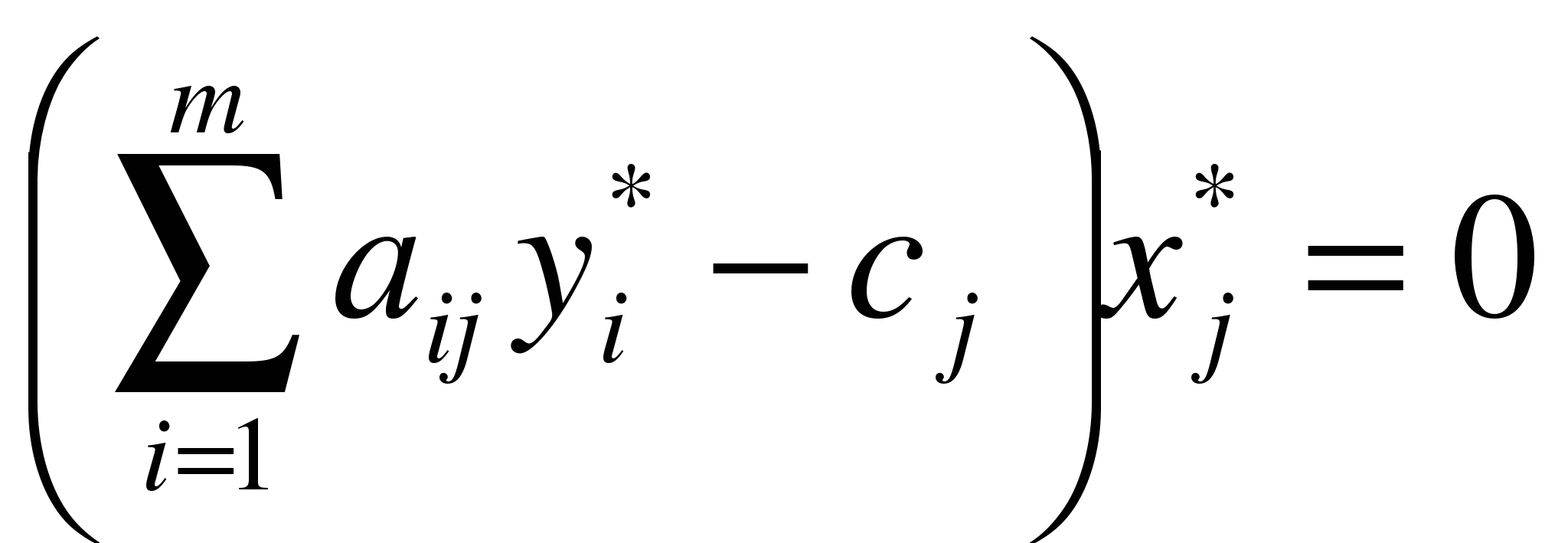
Дата добавления: 2015-04-18; просмотров: 410; Мы поможем в написании вашей работы!; Нарушение авторских прав |