Математическая модель

Ограничимся рассмотрением классической модели дискриминантного анализа, не затрагивая вопросов статистического оценивания его результатов.

Пусть результатом наблюдения над объектом является реализация m-мерного случайного вектора . Известно, что этот объект относится к одной из l генеральных совокупностей, к одному из l классов, относительно которых предполагается:

— каждый класс имеет m-мерное нормальное распределение, , где X ^{(j) —} обозначение вектора X для j-го класса, 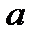_j=MX ^(j), - ковариационная матрица вектора X, общая для всех l классов;

— каждый класс j представлен n_j — выборкой (эти выборки называют обучающими).

Требуется построить правило дискриминации — правило распознавания класса, к которому относится не попавший в выборки объект x ⁽⁰⁾.

На рис. 3 изображены графики функций нормальных плотностей f₁(x) и f₂(x), различающихся только математическими ожиданиями a₁ и a₂.

Рис. 3

Пусть d — некоторая точка на оси Ox и правило дискриминации такое: классифицируемый объект относят к первому классу тогда и только тогда, когда , где x значения CB X у объекта, и ко второму — во всех остальных случаях.

Точку d найдем как решение следующей экстремальной задачи: при условии равенства вероятностей , что равносильно условию

, (41)

требуется минимизировать вероятность

. (42)

Используя метод множителей Лагранжа, нетрудно убедиться в том, что задача (41) ~ (42) равносильна системе, включающей уравнение (41) — требование равенства вероятностей ошибок и уравнение , которое с учетом нормальности распределений и равенства дисперсий, равносильно уравнению

, (43)

где С — некоторая постоянная величина.

В рассматриваемом тривиальном случае из (41) следует, что . Поставив x=d в (43), получим С = 0. И сформулированное выше классификационное правило эквивалентно следующему: объект относят к первому классу тогда и только тогда, когда

, (44)

во всех остальных случаях — по второму.

Для m- мерного случайного вектора X классификационное правило в терминах выборки звучит так: объект с координатами относят к первому классу тогда и только тогда, когда

, (45)

и ко второму — во всех остальных случаях. В соотношении (45): 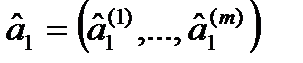- вектор средних значений случайных величин X₁,…, X_m в n₁-выборке из первого класса, — вектор средних значений этих величин в n₂-выборке из второго класса, - рассчитанная по обучающим выборкам оценка ковариационной матрицы вектора X, общей для двух классов. Будем считать, что в n₁-выборку попали объекты с номерами 1, 2,…, n₁, в n₂-выборку — объекты с номерами 1^*, 2^*,…, n₂^*, а x_ij — это значения CB X_j, j=1,…, m, для i-го объекта. Тогда

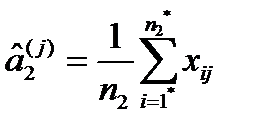, j=1,…, m (46)

, (47)

где 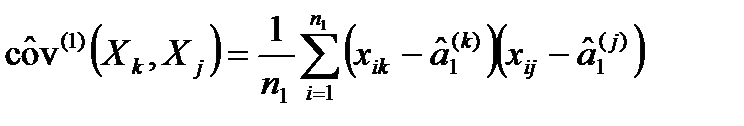, (48)

. (49)

Соотношением (45) задается вид дискриминантной функции для двух нормально распределенных совокупностей.

Методы оптимизации