Задача вариационного исчисления и правило ее решения.

Функционал- это обобщенное понятие функции, т.е. такая функция в которой роль независимой переменной играет другая функция.

Функционал представляет собой определённый интеграл некоторой функции F, которой должна быть непрерывной и иметь непрерывные частные производные по всем координатам.

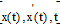
Простейшей задачей вариационного исчисления является задача определения функции х⁰(t), которая бы доставляла экстремум функционалу I и проходила бы через фиксированные точки x₀(t₀), x(t₁) в момент времени t₀, t_1.

Уравнение Эйлера:

Решением равнения Эйлера является функция x⁰(t) доставляющая экстремум функционалу и называемая экстремальной, т.е. для того чтобы определить экстремум функционала I достаточно составить и решить уравнение Эйлера.

Правило решения простейшей задачи вариационного исчисления:

Дан функционал:

Где функция F непрерывна и дифференцируема, а x(t₀) =x₀, x(t₁) =x₁ , следовательно удовлетворяет граничным условиям.

Определить x⁰(t)- экстремаль, доставляющую min функционалу I проходящую через граничные точки при t₁ и t_0.

Правило решения:

1. Формализация задачи

2. Определение необходимого условия существования экстремума с помощью уравнения Эйлера

3. Решение уравнение Эйлера, и определение х⁰(t).

4. Доказательство единственности решения или его отсутствия.