
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА ТРУБОПРОВОДОВ
ДВИЖЕНИЕ ЖИДКОСТИ В НАПОРНЫХ ТРУБОПРОВОДАХ
НАЗНАЧЕНИЕ И КЛАССИФИКАЦИЯ ТРУБОПРОВОДОВ
В современной технике применяются трубопроводы различного назначения, служащие для перемещения разнообразных жидкостей (вода, нефть, глинистые растворы и т. д.) и изготовляемые из разных материалов (металл, бетон, дерево). Наряду с трубопроводами самых незначительных размеров (капилляры), используемыми в лабораторной технике и контрольно-измерительной аппаратуре, имеются трубопроводы протяжением в сотни километров (магистральные нефтепроводы) и диаметром в несколько метров (трубопроводы гидротехнических сооружений).
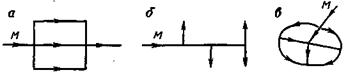
Рис. 160.
В зависимости от конфигурации различают простые и сложные трубопроводы.
Простым трубопроводом называется трубопровод, не имеющий разветвлений на пути движения жидкости от точки забора до точки потребления, сложным — трубопровод, представляющий собой сеть труб, состоящую из основной магистральной трубы и ряда отходящих от нее ответвлений. Сложные трубопроводы делятся на следующие основные виды:
а) параллельное соединение, когда к основной магистрали М подключены параллельно ей еще одна или несколько труб (рис. 160, а);
б) разветвленные трубопроводы, в которых жидкость из магистрали М подается в боковые ответвления и обратно в магистраль не поступает ^рис. 160, б);
в) кольцевые трубопроводы, представляющие собой замкнутую сеть (кольцо), питаемую от основной магистрали М (рис. 160, в).
В сложных трубопроводах различают:
а) транзитный расход, т. е. расход, передаваемый по магистрали;
б) путевой (или попутный), отбираемый из магистрали в ряде промежуточных точек по пути движения жидкости.
При этом расход называется сосредоточенным, если точки отбора располагаются на значительном расстоянии друг от друга, и непрерывным, если эти точки расположены очень близко одна от другой.
ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА ТРУБОПРОВОДОВ
Исходным уравнением для расчета трубопроводов является уравнение Бернулли (см. § 27), из которого, как известно, следует, что разность значений напора Нг в сечении /—/ и Н2 в сечении 2—2 затрачивается на преодоление гидравлических сопротивлений при движении жидкости на участке между этими сечениями. Таким образом,
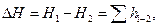
где

При этом потери напора на трение по длине определяются по формуле Дарси—Вейсбаха (4.45)
 (6.1)
(6.1)
или главным образом при расчетах некруглых труб по выражению (4.42)

Местные же потери напора учитываются по формуле (4.68)
 (6.2)
(6.2)
Значения коэффициентов 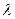 и С определяются по соответствующим формулам, приведенным в § 46, а коэффициенты местных сопротивлений
и С определяются по соответствующим формулам, приведенным в § 46, а коэффициенты местных сопротивлений 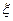 устанавливаются в зависимости от вида сопротивления на основании данных, приведенных в § 50.
устанавливаются в зависимости от вида сопротивления на основании данных, приведенных в § 50.
В дальнейшем мы встретимся с различными видоизменениями расчетных формул, преследующими цель упрощения приемов расчета.
Вспомним выражения для коэффициента 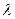 , данные в § 46
, данные в § 46

 (6.3)
(6.3)
при ламинарном режиме,
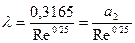 (6,4)
(6,4)
при турбулентном режиме для гладких труб, и то обстоятельство, что при больших значениях Re (т. е. в области «вполне шероховатых» труб при турбулентном режиме) коэффициент 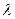 не зависит от Re; сохраняя для
не зависит от Re; сохраняя для 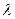 общую зависимость вида (6.3), (6.4), следует в этом случае показатель степени у Re принять равным нулю.
общую зависимость вида (6.3), (6.4), следует в этом случае показатель степени у Re принять равным нулю.
Таким образом, общее выражение для коэффициента 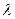 при любых режимах движения жидкости может быть представлено в виде
при любых режимах движения жидкости может быть представлено в виде
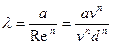 (6.5)
(6.5)
Подставив это выражение в формулу (6.1), будем иметь
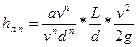 (6.6)
(6.6)
С учетом же того, что
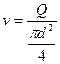
из (6.6) получим следующее общее выражение для потерь напора (формула Л. С. Лейбензона):
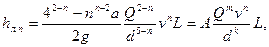 (6.7)
(6.7)
где

 k=5-n
k=5-n
Если выражать все входящие в эту формулу величины в технической системе единиц (килограмм-силах, метрах, секундах), то коэффициент А и показатели степени m, n и k будут иметь значения, приведенные в табл. 41.
Таблица 41
Значения коэффициента А и показателей степени m, n и k в формуле (6.7)

Для непосредственного определения расхода из выражения (6.7) получаем
 (6.8)
(6.8)
где приняты обозначения
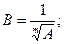
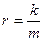
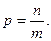
Значения коэффициента В и показателей rи р в этой формуле при различных режимах течения жидкости приведены в табл. 42.
Таблица 42
Значения коэффициента В и показателей степени rи р в формуле (6.8)

Следовательно, при квадратичном законе сопротивления формула (6.8) может быть переписана так:
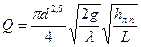
Введем далее обозначение
 (6.9)
(6.9)
Тогда получим
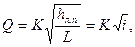
или
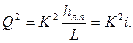 (6.10)
(6.10)
Величина K в этой формуле называется модулем расхода.
Формула (6.10) очень проста и поэтому часто применяется для практических расчетов в области турбулентного режима при квадратичном законе сопротивления. Последний же соответствует движению жидкости при больших значениях числа Рейнольдса, что практически обычно имеет место в водопроводах. Ввиду этого указанную формулу часто называют «водопроводной формулой».
При i = 1 из формулы (6.10) следует
Q = K.
Таким образом, модуль расхода представляет собой расход жидкости при уклоне, равном единице.
Исходя из формулы Шези (4.43), для расхода можно получить также выражение
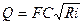
Сопоставляя его с формулой (6.9), видим, что модуль расхода K, выраженный через коэффициент С, имеет вид
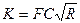 . (6.11)
. (6.11)
Таким образом, значения модуля расхода определяются диаметром трубы и зависят от коэффициентов 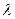 в формуле (6.9) или С в формуле (6.11). В табл. 43 приведены значения модуля расхода К для чугунных труб различных диаметров, подсчитанные по формуле (6.11), где коэффициент С принимался по формуле Маннинга
в формуле (6.9) или С в формуле (6.11). В табл. 43 приведены значения модуля расхода К для чугунных труб различных диаметров, подсчитанные по формуле (6.11), где коэффициент С принимался по формуле Маннинга
(4.58) равным 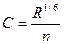 , а коэффициент шероховатости п = 0,0125
, а коэффициент шероховатости п = 0,0125
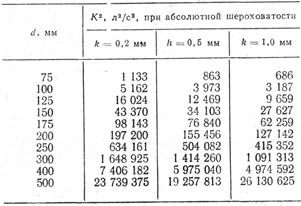
(что соответствует случаю чугунных труб); в табл. 44 даны значения K2, подсчитанные по формуле (6.9), где значения 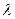 определялись по формуле Прандтля—Никурадзе (4.50) при абсолютной шероховатости 0,2; 0,5 и 1,0 мм.
определялись по формуле Прандтля—Никурадзе (4.50) при абсолютной шероховатости 0,2; 0,5 и 1,0 мм.
Таблица 43
Значения модуля расхода для чугунных труб

Таблица 44
Значения модуля расхода для труб различной шероховатости
Для случаев, когда квадратичный закон сопротивления недействителен (обычно в нефтепроводах), упрощенные зависимости, удобные для практических расчетов, можно получить следующим образом. Будем исходить из общей формулы (6.7) и обозначим в ней 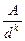 через Kd (коэффициент сечения), vп через Kv (вязкостный коэффициент), Qm через KQ (расходный коэффициент). Тогда получим следующую запись формулы для гидравлического уклона
через Kd (коэффициент сечения), vп через Kv (вязкостный коэффициент), Qm через KQ (расходный коэффициент). Тогда получим следующую запись формулы для гидравлического уклона
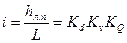 (6.12)
(6.12)
где при турбулентном режиме в области «гладких» труб (т. е. в области применимости формулы Блазиуса, при Re 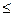 100 000)
100 000)
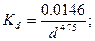
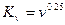
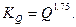
При ламинарном режиме эта формула может быть представлена в еще более простом виде. На самом деле, так как в этом случае п = 1 и т = 1, для ламинарного режима получаем
i = KddvQ, (6.13)
где

В табл. 45 приведены (для труб различных диаметров) значения коэффициента сечения Kd при ламинарном режиме и турбулентном режиме в области гладких труб; в табл. 46 и 47 даются значения коэффициентов Kv и KQ при турбулентном режиме для той же области.
Таблица 45 Значения коэффициента сечения Kd
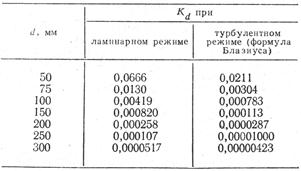
Таблица 46 Значения вязкостного коэффициента Kv
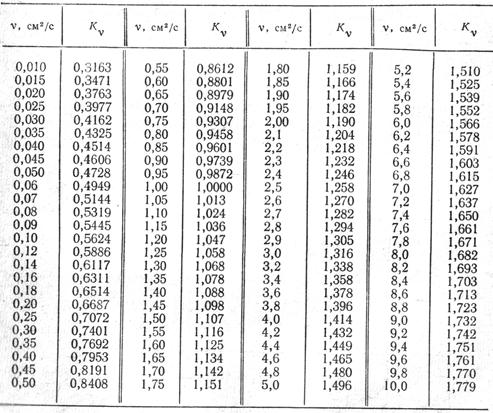
Таблица 47
Значения расходного коэффициента Kq
| Q, л/с | KQ | Q, л/с | KQ | Q, л/с | KQ | Q, л/с | KQ | Q, л/с | KQ | Q, л/с | KQ |
| 0,2 | 0,05982 | 5,2 | 17,91 | 10,5 | 61,25 | 299,3 | 973,4 | ||||
| 0,4 | 0,2011 | 5,4 | 19,13 | 66,43 | 319,8 | ||||||
| 0,6 | 0,4088 | 5,6 | 20,38 | 11,5 | 71,81 | 340,9 | |||||
| 0,8 | 0,6776 | 5,8 | 21,67 | 77,37 | 362,5 | ||||||
| 12,5 | 83,1 | 384,5 | |||||||||
| 1,2 | 1,376 | 6,2 | 24,36 | 88,98 | 407,3 | ||||||
| 1,4 | 1,802 | 6,4 | 25,75 | 13,5 | 95,06 | 430,4 | |||||
| 1,6 | 2,275 | 6,6 | 27,17 | 101,3 | 454,3 | ||||||
| 1,8 | 2,798 | 6,8 | 28,63 | 14,5 | 107,7 | 478,7 | |||||
| 3,363 | 30,12 | 114,2 | 503,7 | ||||||||
| 2,2 | 3,974 | 7,2 | 31,64 | 15,5 | |||||||
| 2,4 | 4,64 | 7,4 | 33,19 | ||||||||
| 2,6 | 5,324 | 7,6 | 34,78 | 16,5 | 581,6 | ||||||
| 2,8 | 6,062 | 7,8 | 36,41 | 142,3 | 608,7 | ||||||
| 6,837 | 38,05 | 17,5 | 149,7 | 636,3 | |||||||
| 3,2 | 7,654 | 8,2 | 39,73 | 157,3 | 664,3 | ||||||
| 3,4 | 8,513 | 8,4 | 41,45 | 18,5 | 692,8 | ||||||
| 3,6 | 9,408 | 8,6 | 43,19 | 172,9 | 722,1 | ||||||
| 3,8 | 10,34 | 8,8 | 44,97 | 19,5 | 180,9 | 751,8 | |||||
| 11,31 | 46,75 | 189,1 | 781,8 | ||||||||
| 4,2 | 12,32 | 9,2 | 48,59 | 205,9 | 812,6 | ||||||
| 4,4 | 13,37 | 9,4 | 50,45 | 223,4 | 843,7 | ||||||
| 4,6 | 14,45 | 9,6 | 52,36 | 241,5 | 875,2 | ||||||
| 4,8 | 15,56 | 9,8 | 54,27 | 261,3 | 907,4 | ||||||
| 16,72 | 56,23 | 279,4 | 940,1 |
Если при движении жидкости в трубопроводе имеет место турбулентный режим в доквадратичной области шероховатых труб (практически весьма часто встречающийся случай), когда 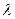 = f(
= f( 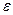 , Re), для расчета могут быть использованы установленные выше зависимости для квадратичного закона сопротивления с введением в них поправочного коэффициента
, Re), для расчета могут быть использованы установленные выше зависимости для квадратичного закона сопротивления с введением в них поправочного коэффициента 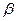 — на «неквадратичность».
— на «неквадратичность».
По-прежнему будем исходить из основной формулы Дарси— Вейсбаха (6.1); произведем в ней замену  умножим и разделим правую часть на
умножим и разделим правую часть на 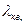 . Тогда получим
. Тогда получим
 (6.14)
(6.14)
где 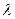 — действительный коэффициент гидравлического сопротивления рассматриваемого трубопровода;
— действительный коэффициент гидравлического сопротивления рассматриваемого трубопровода; 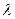 кв — коэффициент гидравлического сопротивления того же трубопровода при квадратичном законе сопротивления.
кв — коэффициент гидравлического сопротивления того же трубопровода при квадратичном законе сопротивления.
Учитывая далее выражение (6.9) и обозначая 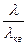 через
через 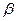
(поправочный коэффициент на «неквадратичность»), вместо формулы (6.14) будем иметь общее соотношение
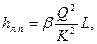 (6.15)
(6.15)
удобное для расчета трубопроводов в доквадратичной области турбулентного режима.
Для определения поправочного коэффициента на «неквадратичность» воспользуемся известными нам формулами для коэффициента гидравлического сопротивления (см. § 46), например формулой Альтшуля (4.53) — для доквадратичной области шероховатых труб и формулой Шифринсона (4.56) — для квадратичной области турбулентного режима.
При этом найдем
 (6.16)
(6.16)
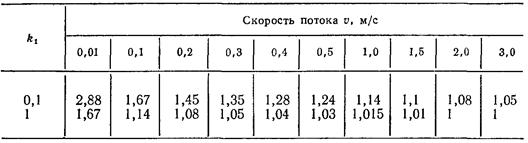
В табл. 48 приведены значения коэффициента 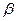 , вычисленные по формуле (6.16) при движении воды (v = 0,01 Ст) в трубах с эквивалентной шероховатостью 0,1 и 1 мм, при различных значениях средней скорости потока v, м/с.
, вычисленные по формуле (6.16) при движении воды (v = 0,01 Ст) в трубах с эквивалентной шероховатостью 0,1 и 1 мм, при различных значениях средней скорости потока v, м/с.
Значения этого коэффициента могут быть легко табулированы и для других случаев.
Таблица 48 Значения поправочного коэффициента 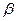 на «неквадратичность»
на «неквадратичность»
§ 68. ОСНОВНЫЕ ЗАДАЧИ ПРИ РАСЧЕТЕ И ПРОЕКТИРОВАНИИ ТРУБОПРОВОДОВ
В первоначальной и наиболее общей постановке задачи при проектировании трубопроводов обычно задаются расход жидкости и положения начального и конечного пунктов трубопровода; в случае сложного трубопровода задача соответственно усложняется заданием ряда расходных пунктов и расходов на отдельных участках. В результате проведения топографических изысканий и сопоставления отдельных возможных вариантов на плане местности наносят трассу и строят продольный профиль трубопровода. Таким образом, при гидравлическом расчете оказываются известными также длина трубопровода и все его высотные отметки. Определению подлежат диаметр трубопровода и напор в его начальном сечении.
Рассматриваемая задача допускает множество решений, так как при прочих равных условиях диаметр одновременно определяет и потери напора: чем меньше диаметр, тем больше потери и, наоборот, чем больше диаметр, тем потери меньше. Поэтому при решении исходят из требований оптимальности и технической целесообразности сооружения и эксплуатации трубопровода.
Меньшие диаметры требуют значительно меньших капитальных затрат на сооружение трубопровода. Стоимость труб, объем земляных работ и работ по укладке труб тем меньше, чем меньше диаметр. Однако уменьшение диаметра трубопровода приводит к увеличению потерь напора, а следовательно, и к увеличению мощности насосов и двигателей, их стоимости и эксплуатационных расходов. Экономически наиболее выгодный диаметр должен соответствовать наименьшей полной стоимости трубопровода, зависящей от капитальных затрат на сооружение и прокладку самого трубопровода, расходов на сооружение насосных станций и эксплуатационных расходов.
По В. С. Яблонскому, приближенно можно принять, что экономически наивыгоднейший диаметр обычно соответствует скоростям течения жидкости примерно 1 м/с, т. е. диаметру, определяемому по формуле
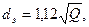
где при расходе жидкости Q, выраженном в м3/с, диаметр dэ получается в м.
Для более точного определения экономически наивыгоднейшего диаметра существует ряд методов, изучаемых в специальных курсах по проектированию и сооружению трубопроводов. В основе этих методов лежит следующий прием. Составляют выражение для полной стоимости трубопровода, включая как капитальные затраты на его сооружение и прокладку, так и эксплуатационные расходы, выраженные в функции от диаметра трубопровода. Затем находят минимум этой функции, т. е. берут первую производную от стоимости по диаметру и приравнивают нулю; из получаемого таким образом уравнения определяют диаметр трубопровода, соответствующий минимуму его полной стоимости.
Искомое значение диаметра может быть определено также графическим способом; при этом по одной координатной оси (рис. 161), например оси абсцисс, откладывают диаметры трубопровода d, а по оси ординат — соответствующие этим диаметрам стоимости s — капитальные затраты (кривая 1) и эксплуатационные расходы (кривая 2). Далее суммированием ординат этих кривых находят полную стоимость трубопровода (кривая 3)., имеющую минимум в некоторой точке а, которая и определяет величину экономически наивыгоднейшего диаметра dэ.
Помимо основной задачи, рассмотренной выше в общей постановке, при гидравлическом расчете трубопроводов могут встретиться также следующие частные задачи:
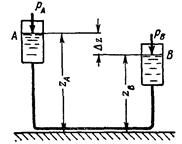
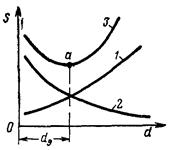
Рис. 161. Рис. 162.
1) определение перепада напора, необходимого для пропуска заданного расхода жидкости по данному трубопроводу;
2) определение расхода жидкости по данному трубопроводу при заданном перепаде напора;
3) определение необходимого диаметра трубопровода для пропуска данного расхода при известном перепаде напора.
Затруднения при решении некоторых задач могут встретиться в случае, если число Рейнольдса невелико, т. е. коэффициент 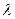 зависит от Re; последнее же становится известным лишь по окончании расчета.
зависит от Re; последнее же становится известным лишь по окончании расчета.
Решения указанных задач рассматриваются в следующих параграфах.
Дата добавления: 2015-04-18; просмотров: 1373; Мы поможем в написании вашей работы!; Нарушение авторских прав |