СЛОЖНЫЕ ТРУБОПРОВОДЫ

Расчет сложных трубопроводов не входит в содержание общего курса гидравлики и обычно изучается в специальных курсах во­доснабжения или проектирования трубопроводов. Поэтому здесь рассматриваются только простейшие примеры сложных трубо­проводов и приводятся лишь основы их гидравлического расчета .

Все решения даются применительно к квадратичному закону сопротивления (местные сопротивления при расчетах не учиты­ваются). Правильность этого предположения может быть в даль­нейшем проверена, и полученные результаты уточнены. При этом для всех участков рассматриваемых трубопроводов определяют числа Рейнольдса, по ним уточняют значения коэффициентов гидравлического сопротивления 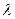и находят соответствующие уточ­ненные значения модулей расхода К; местные сопротивления учи­тывают введением эквивалентных длин.

В случае параллельного соединения трубопроводов (рис. 164) магистральный трубопровод в некоторой точке В разветвляется на несколько параллельных линий труб 2, 3, 4, ..., сходящихся затем опять вместе в одной общей точке магистрали С.

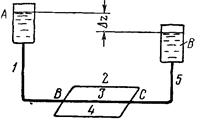
Рис.164.

Пусть длины и диаметры отдель­ных участков подобного трубопро­вода, в том числе и параллельно включенных линий, будут L_ъ L₂, L₃, Li, L_b и d_x, d_i7 d_s, d₄, 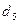Рас­ходы соответственно обозначим: в

магистрали — через Q₁ = Q₅ = Q, а в параллельных линиях через Q₂, Q₃ и Q₄. При этом, очевидно, что расход в магистрали

Q = + Q_s + . (6.26)

Имея в виду, что значения напора в точках разветвления В и С одинаковы для всех параллельно включенных линий, приходим к выводу, что потери напора в них должны быть одинаковы, неза­висимо от того, для какой линии их подсчитывать. Таким обра­зом,

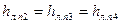(6.27)

ИЛИ

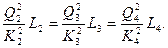(6 28)

Решая совместно уравнения (6.26) и (6.28), можно найти искомые расходы. Так, из уравнений (6.28) имеем

Подставляя затем эти значения в уравнение (6.26), получаем

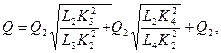
откуда находим

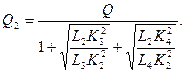
Аналогично находят и остальные расходы.

Рассматриваемый в целом трубопровод, изображенный на рис. 164, представляет собой последовательное соединение от­дельных участков: участка магистрали 1, участка включенных в магистраль параллельных линий труб 2, 3, 4 и участка маги­страли 5. Полная потеря напора в этом случае определяется так же, как и в обычном последовательном соединении, т. е. как сумма потерь на отдельных участках. При этом необходимо иметь в виду, что потери напора в параллельных линиях не складываются,

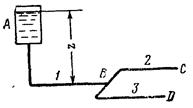
Рис. 165. Рис. 166.

а в уравнение потерь вследствие равенства (6.27) вводится только потеря напора в одной из этих линий, безразлично какой, напри­мер линии 2. Поэтому

(6.29)

Изложенное позволяет наметить схемы гидравлического рас­чета и для других видов сложных трубопроводов.

Для простейшего разветвленного трубопровода (рис. 165), в котором участки 1 и 2 (также 1 я 3) соединены между собой по­следовательно, а участки 2 и 3 включены параллельно и истече­ние в точках С и D, расположенных в одной горизонтальной пло­скости, происходит в атмосферу, по аналогии с предыдущим имеем

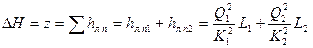
ИЛИ

причем, так как

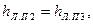
то

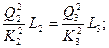
кроме того,

=Q₂ + Q₃.

Если точки С и D расположены в разных горизонтальных пло­скостях (рис. 166), аналогичная система уравнений получает вид

Кроме того, имеем

=Q₂ + Q₃.

И

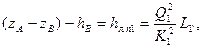
где h_в — пьезометрический напор, соответствующий давлению в точке В и определяемый из выражений

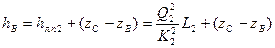
или

Совместное решение полученных уравнений позволяет найти искомые Q₂, Q₃ и Q₁.

Кольцевые трубопроводы рассчитывают по такой же схеме, что и при параллельном соединении. Так, в случае параллельного соединения, в котором расходный пункт С питается с двух сторон (рис. 167), как и ранее, имеем

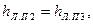
=Q₂ + Q₃.

Задача усложняется, если в трубопроводе имеется несколько расходных пунктов, например в простейшем случае кольцевого трубопровода (рис. 168). При этом задаются значениями расходов 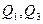и направлением движения жидкости в отдельных уча­стках кольца 2, 3, 4 я вычисляют потери напора от общей точки разветвления В до расходных пунктов С и D. Если в первом пред­положении принять, например, что точка С питается только с одной стороны, а точка D — с двух сторон, то, как это следует из свойств параллельного соединения, необходимо, чтобы потеря напора научастке 4 равнялась сумме потерь на участках 2 и 3

Рис. 167.

Расчет производится до тех пор, пока путем изменений значений расхода и нап­равления движения жидкости не будет дос­тигнуто указанное равенство потерь. Рассмотрим также трубопровод, на некотором участке которого имеется непрерывный путевой расход (рис. 169). Длину этого уча­стка АВ обозначим L, проходящий по нему транзитный расход — Q_T, путевой расход — Q_n; при этом примем, что путевой расход по всей длине L распределяется равномерно, т. е. на единице

длины участка АВ равен q =

Определим потери напора на участке А В с непрерывным путе­вым расходом.

Рис. 168. Рис. 169.

Расход в некотором произвольном сечении этого участка С, расположенном на расстоянии х от начального сечения А, будет меньше расхода в сечении А, равного Q_T + 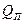на величину отбора на длине х—qx и составит

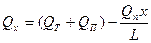
Полагая по-прежнему, что движение жидкости происходит в квадратичной области турбулентного режима, для потери напора на элементарном участке трубопровода длиной dx у сечения С будем иметь

Интегрируя далее это выражение в пределах от 0 до L, полу­чаем расчетную формулу для определения потери напора на всем участке трубопровода длиной L, на котором имеет место непре­рывный путевой расход,

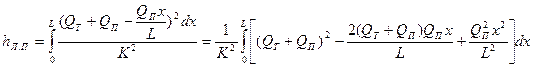
или окончательно

В частном случае, когда на участке L отбирается весь расход, т. е. транзитный расход Q_T = 0, потеря напора будет

Эта формула известна под названием формулы Дюпюи. Из нее следует, что потери напора в трубопроводе при непрерывном пу­тевом расходе оказываются в 3 раза меньше той потери напора, которая имела бы место при отсутствии путевой раздачи и таком же расходе, полностью сосредоточенном в конце трубопровода.

Аналогичная зависимость для ламинарного режима была полу­чена Е. 3. Рабиновичем. В этом случае потеря напора при непре­рывном путевом расходе будет в 2 раза меньше, чем при равном ему расходе сосредоточенном в конце трубопровода.