ЗАДАЧА О ПРОСТОМ ТРУБОПРОВОДЕ

Пусть (рис. 162) имеются два резервуара: питающий А и рас­ходующий В с установившейся разностью уровней 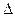z = z_A — z_B, соединенные между собой простым трубопроводом длиной L постоянного диаметра d (в других случаях роль верхнего резер­вуара может выполнять насос, установленный в начале трубопровода и создающий там давление pgz_A, где р — плотность жидкости; нижний резервуар также может отсутствовать, и жидкость может вытекать прямо в атмосферу через отверстие в конце трубопро­вода).

Пусть резервуары открыты и давление на свободной поверх­ности жидкости в них равно атмосферному. Средние скорости в се­чениях на поверхности жидкости в резервуарах обозначим через

Составим для указанных сечений уравнение Бернулли

Пренебрегая в этом уравнении значениями скоростных напоров и вследствие их малости по сравнению с остальными величинами, а также учитывая, что р_А = р_В, получаем

Полная потеря напора определяется как сумма потерь на тре­ние по длине трубопровода

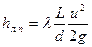
и местных потерь ¹

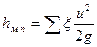
Следовательно,

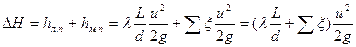
или

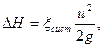
где коэффициент 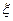_сист = называют - также коэффи­циентом сопротивления трубопровода (системы).

Из последнего уравнения по заданному 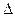Н легко определить скорость и расход жидкости

(6.17)

(6.17 )

При квадратичном законе сопротивления ( 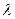, не зависит от числа Рейнольдса) и большой длине трубопровода, когда местными потерями можно пренебречь, расход определяется непосредственно из формулы (6.10)

(6.18)

В тех случаях, когда необходимо определить диаметр трубо­провода (перепад напора и расход жидкости известны), из этой же формулы находят модуль расхода и по соответствующим таблицам (см., например, табл. 43 и 44) уста­навливают стандартный диаметр трубо­провода, отвечающий ближайшему (к полученному расчетом) большему зна­чению этого модуля.

Если рассматриваемый трубопровод состоит из ряда отдельных участков 1, 2, 3, ..., л различной длины L_1, L₂, ..., L_n и разного диаметра d, d₂, .... d_n, последовательно соединен­ных между собой (рис. 163), задача решается аналогично пре­дыдущему.

Рис. 163

При таком последовательном соединении полная потеря напора на всем протяжении трубопровода, от начальной его точки А до конечной В, определяется как сумма потерь на участках

и может быть выражена через коэффициент сопротивления системы следующим образом:

(6.19)

где U1 — скорость в каком-нибудь произвольно выбираемом се­чении трубопровода, а коэффициент сопротивления системы

(6.20)

При неучете местных потерь и квадратичном законе сопроти­вления

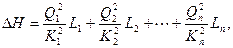
откуда, принимая во внимание, что в простом трубопроводе

Q₁ = Q₂ = ... = = Q,

находим

и легко определяем искомый расход жидкости

(6.21)

Иногда расчетным уравнениям придают вид

(6.22)

и называют величину А коэффициентом пропускной способности трубопровода.

Сравнивая между собой выражения (6.18) и (6.22), нетрудно установить зависимость между коэффициентом пропускной спо­собности и модулем расхода

(6.23)

Для данного трубопровода коэффициент пропускной способ­ности всегда имеет вполне определенное постоянное значение и при заданном напоре полностью определяет пропускаемый рас­ход.

Из выражения (6.22) также следует

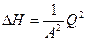, (6.24)

или

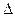Н = ВQ². (6.25)

Коэффициент В = в этом уравнении характеризует собой

гидравлические сопротивления трубопровода и поэтому может быть назван его характеристическим коэффициентом.

При неквадратичном законе сопротивления гидравлические рас­четы трубопроводов рекомендуется выполнять на основании зави­симостей, установленных в предыдущем параграфе.