
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приборы для измерения давления
 Жидкостные манометры обычно представляют собой изогнутые U-образные стеклянные трубки диаметром 10-15 мм, присоединяемые одним концом к точке, где требуется измерить давление, второй конец остается открытым (рис. 7.9). Очевидно, что жидкость только тогда будет в равновесии, когда вследствие разности уровней в сосудах возникает противодавление ρgh, уравновешивающее разность давлений
Жидкостные манометры обычно представляют собой изогнутые U-образные стеклянные трубки диаметром 10-15 мм, присоединяемые одним концом к точке, где требуется измерить давление, второй конец остается открытым (рис. 7.9). Очевидно, что жидкость только тогда будет в равновесии, когда вследствие разности уровней в сосудах возникает противодавление ρgh, уравновешивающее разность давлений 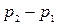 . Из условия равновесия следует Рис. 7.9
. Из условия равновесия следует Рис. 7.9
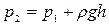 ,
,
где h – разность уровней жидкости в сообщающихся сосудах; ρ – плотность жидкости; g – ускорение свободного падения. На плоском щите позади трубок обычно монтируется шкала, по которой возможно измерить высоту поднятия жидкости под действием давления. Такие манометры применяются для измерения небольших давлений – от 1 до 10 кПа. Для измерения больших давлений потребовались бы слишком высокие пьезометрические трубки. Так, для измерения давления 0,15 МПа (1,5 атм) необходима трубка высотой 15 м. Для измерения таких давлений в жидкостные манометры заливают более тяжелые жидкости, например, ртуть; высота h в этом случае будет в 13,6 раза меньше. Для измерения ещё больших давлений (или глубокого вакуума) применяют пружинные манометры.
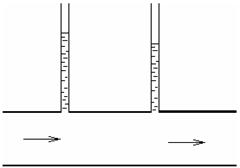 Пример 7.3.Для измерения потерь напора (энергии) часто применяют пьезометры (рис. 7.10), присоединяемые к отверстиям в стенке трубы.
Пример 7.3.Для измерения потерь напора (энергии) часто применяют пьезометры (рис. 7.10), присоединяемые к отверстиям в стенке трубы.
Связь между напором и давлением. Отношение давления 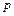 к произведению ρg (ρ- плотность данной жидкости) имеет размерность длины и выражается в метрах или сантиметрах
к произведению ρg (ρ- плотность данной жидкости) имеет размерность длины и выражается в метрах или сантиметрах
 . (7.15)
. (7.15)
Рис. 7.10 таким образом последнее равенство устанавливает связь между давлением и некоторой длиной Н, которая называется напором. Если трубку с открытым верхним концом присоединить к потоку в трубе, рис.7.11, в котором давление больше атмосферного, то вода в трубке поднимется на некоторую высоту Н', которая определится так
 ,
,
где pизб - избыточное давление в данном сечении трубы; ρ – плотность жидкости. Этот прием является способом выражать давление высотой столба данной жидкости. Например, давление 1 ат = 98000 Н/м2 =98000 Па будет соответствовать высоте водяного столба
 м.вод.ст.
м.вод.ст.
Иногда говорят вместо давления – напор, например, напор в сети равен 10 м (он соответствует давлению 1 ат); при этом если к трубе присоединить тонкую вертикальную трубку, то в ней вода поднимется на высоту 10 м (рис. 7.12).
|

Рис. 7.11 Рис. 7.12
Задача 7.4. Определить высоту h поднятия воды в запаянной с одного конца трубке, опущенной в сосуд с водой при нормальном атмосферном давлении на ее поверхности, если над поверхностью воды в трубке будет безвоздушное пространство с давлением p=0.
Решение. Представив в поперечном сечении трубки на уровне свободной поверхности тонкую площадку, рассмотрим условие равновесия всех сил, действующих на эту площадку. Сверху на нее будет действовать только гидростатическое давление от столба высотой h, p=ρgh. Снизу на эту площадку будет передаваться атмосферное давление pа=ρgh и искомая величина равна
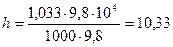 м.
м.
Такую величину имеет столб воды, создающий давление нормальной атмосферы. Рассмотренная трубка является известным прибором – барометром. Для измерения величины атмосферного давления неудобно применять трубки высотой 10,33 м и поэтому в качестве жидкости в них применяется ртуть, имеющая плотность, в 13,6 раз большую, чем вода.
Задача 7.5. Определить высоту поднятия ртути в ртутном барометре. Принять pа=1,033 кг/см2, плотность ртути 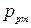 =13600 кг/м3.
=13600 кг/м3.
 7.6. Напор. Удельная потенциальная энергия
7.6. Напор. Удельная потенциальная энергия
 При выводе (7.5) верхнее основание параллелепипеда совпадало со свободной поверхностью жидкости, но это совсем не обязательно; верхнее основание может находиться на любой глубине (рис. 7.13). Плоскость отсчета расстояний z по вертикали в проекции на плоскость рисунка превратится в горизонтальную ось О-О.
При выводе (7.5) верхнее основание параллелепипеда совпадало со свободной поверхностью жидкости, но это совсем не обязательно; верхнее основание может находиться на любой глубине (рис. 7.13). Плоскость отсчета расстояний z по вертикали в проекции на плоскость рисунка превратится в горизонтальную ось О-О.
 Из рис. 7.13 следует (учитывая (7.5)), что
Из рис. 7.13 следует (учитывая (7.5)), что
 . (7.16)
. (7.16)
Из последнего уравнения для двух частиц из одного и того же объема жидкости в сосуде с z1 и z2 получаем
 . (7.17)
. (7.17)
Так как z1 и z2 были выбраны Рис. 7.13
произвольно, то для данного объема имеем
 . (7.18)
. (7.18)
Величина Н называется пьезометрическим напором.
Геометрический смысл (7.18) состоит в том, что сумма геометрической z и пьезометрической высот p/  есть величина, постоянная для данного объема жидкости. Энергетический смысл (7.18) состоит в том, что удельная потенциальная энергия
есть величина, постоянная для данного объема жидкости. Энергетический смысл (7.18) состоит в том, что удельная потенциальная энергия 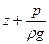 в каждой точке данного объема есть величина постоянная. Удельной потенциальной энергиейназывается энергия частицы жидкости, отнесенная к единице веса.
в каждой точке данного объема есть величина постоянная. Удельной потенциальной энергиейназывается энергия частицы жидкости, отнесенная к единице веса.
Дата добавления: 2015-04-18; просмотров: 284; Мы поможем в написании вашей работы!; Нарушение авторских прав |