
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 7.2. Гидравлический пресс.
Гидравлический пресс создает посредством жидкости усилие, способное произвести на коротком пути большую работу.
 Гидравлический пресс (рис. 7.3) состоит из цилиндра 1 и поршня 2 с платформой 3, на которой помещено тело 4, например, кубик при испытании материалов. По трубке 5 в цилиндр 1 пресса подается жидкость под давлением p, создаваемым различными способами. Обозначая площадь сечения поршня 2 буквой ω1 , получим величину силы давления на поршень
Гидравлический пресс (рис. 7.3) состоит из цилиндра 1 и поршня 2 с платформой 3, на которой помещено тело 4, например, кубик при испытании материалов. По трубке 5 в цилиндр 1 пресса подается жидкость под давлением p, создаваемым различными способами. Обозначая площадь сечения поршня 2 буквой ω1 , получим величину силы давления на поршень
P1=pω1 . (7.10)
Эта сила сжимает тело 4. постоянное давление p в трубке 5 может быть создано, например, насосом, состоящим из цилиндра 6, в котором движется малый поршень 7. цилиндр имеет два отверстия: отверстие 8 с клапаном, открывающимся внутрь цилиндра, и отверстие 9 с клапаном, Рис. 7.3
открывающимся наружу. Через отверстие 8 жидкость засасывается в цилиндр 6 при поднятии малого поршня 7. В этот момент клапан 8 открыт, а клапан 9 закрыт. Через отверстие 9 жидкость выдавливается из цилиндра 6 в трубку 5 и далее в цилиндр 1 при опускании малого поршня. В этот момент клапан 9 открыт, а клапан 8 закрыт.
Обозначая ω2 площадь сечения малого поршня, а P2 - силу давления на малый пор  шень, получим величину давления в цилиндрах 1 и 6 и трубке 5:
шень, получим величину давления в цилиндрах 1 и 6 и трубке 5:
 .
.
Подставляя это значение р в формулу (7.10), имеем
 . (7.11)
. (7.11)
Таким образом, на рабочий поршень передается сила, во столько раз большая силы давления от малого поршня 7, во сколько больше раз площадь сечения поршня. На практике сила R, сжимающая тело 4, вслед- Рис. 7.4
ствие трения меньше Р1.
Это учитывается введением в формулу коэффициента полезного действия η, принимаемого обычно равным 0,85. Следовательно, расчетная формула гидравлического пресса будет
 . (7.12)
. (7.12)
Гидравлический аккумулятор. Гидравлический аккумулятор применяется для выравнивания давления и расхода жидкости в гидравлических установках. В периоды малых расходов он накапливает жидкость, поступающую от насосов, в периоды больших расходов отдает ее рабочим машинам.
Гидравлический аккумулятор (рис. 7.4) состоит из цилиндра, в котором ходит поршень 2 с площадью поперечного сечения ω. На верхний конец поршня действует груз P, в результате чего в цилиндре 1 создается давление р=P/ω, которое и передается по закону Паскаля к гидравлическим машинам по трубе 4. В аккумулятор жидкость поступает от насоса по трубе 3. если количество жидкости, поступающей в цилиндр аккумулятора, больше количества используемой жидкости, то поршень 2 будет подниматься; если же, наоборот, количество притекающей жидкости меньше количества уходящей, то поршень 2 будет опускаться. Однако в этих случаях давление в аккумуляторе, а следовательно, и во всей системе, которую он питает, будет оставаться постоянным.
Задача 7.3. Определить усилие, которое развивает гидравлический пресс, имеющий D=250 мм, d=25 мм, если усилие, приложенное к малому поршню, равно 200 Н. Коэффициент полезного действия пресса η = 0,8.
Решение. Искомое усилие равно
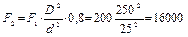 Н.
Н.
Дата добавления: 2015-04-18; просмотров: 377; Мы поможем в написании вашей работы!; Нарушение авторских прав |