Гидростатическое давление и его свойства. Напомним, что в разделе гидростатики исследуется жидкость, нахо­дящаяся в состоянии равновесия (или относительного покоя)

Напомним, что в разделе гидростатики исследуется жидкость, нахо­дящаяся в состоянии равновесия (или относительного покоя), скорости движения и угловые скорости сдвига равны нулю. В этом случае сопро­тивляемость жидкости сдвигающим и растягивающим усилиям отсутству­ет.

Введем понятие гидростатического давления.

Рассмотрим произвольный объем жидкости, находящийся в равнове­сии (рис. 2.1). Мысленно рассечем его плоскостью ВС на две части I и II,первую мысленно отбросим. Для сохранения равновесия второй части суммарное воздействие на нее отсеченной части заменим силой Р

.Пусть площадь всей плоскости разреза равна со. Тогда среднее гид­ростатическое давление на площади ВС

Р ср=P/ω

Для того, чтобы определить давление в точке А, выделим вокруг нее малую площадку ∆ω, сила, приходящаяся на эту площадку - ∆Р. Гидростатическим давлением в точке А называется предел

Из определения текучести среды следует, что в состоянии покоя в жидкости касательные напряжения равны нулю, и в каждой точке произ­вольно ориентированной в пространстве площадки действуют только нор­мальные напряжения. Отсюда вытекает первое свойство гидростатическо­го давления: гидростатическое давление всегда совпадает с направлением внутренней нормали к рассматриваемой площадке.

Предположим обратное - что сила гидростатического давления на­правлена не по нормали к поверхности выделенного объема. Тогда ее можно разложить на нормальную и касательную составляющие. Но каса­тельная составляющая вызвала бы скольжение жидкости вдоль поверхно­сти. А мы рассматриваем случай покоящейся жидкости, т. е. неподвижной и находящейся в равновесии. Значит, на поверхности существуют только нормальные составляющие давления. Более того, они направлены внутрь рассматриваемого объема (иначе на поверхности возникли бы растяги­вающие напряжения, а их жидкости не воспринимают), следовательно, яв­ляются сжимающими.

Второе свойство гидростатического давления состоит в следующем: величина гидростатического давления в данной точке не зависит от на­правления той площадки, на которую оно действует.

Рис. 2.2

Направление площадки будем характеризовать направлением нор­мали к ней. Второе свойство давления означает, что если через одну точку внутри жидкости провести две по-разному ориентированные площадки

Ipec. 2.2), то гидростатические давления р₁ и р₂, действующие на этих площадках, по величине будут одинаковы, т. е. \р1| = \р₂\.

Для доказательства второго свойства давления выделим в непод­вижной жидкой среде элементарный объем в форме тетраэдра (рис. 2.3) с ребрами, параллельными координатным осям и соответственно равными dx, dy, dz.

Доказательство:

1. Проведём произвольным образом плоскость. Эта плоскость при пересечении с координатными плоскостями образует тетраэдр (рис 2.3).

2. Пусть давление на вершине тетраэдра , (где px, py, pz – проекции давления на соответствующие оси). Давление изменяется вдоль осей по некоторому закону.

Тогда давление в центре площадки левой грани равно ,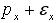

где εx – бесконечно малая добавка, характеризует изменение давления при перемещении от вершины тетраэдра к центру площадки левой грани.

Давление в центре площадки нижней грани равно .

Давление в центре площадки дальней грани равно .

Давление в центре грани n равно . (εz, εy, εn – бесконечно малые добавки, аналогично εx.)

3. Составим уравнение равновесия для проекции сил на ось ОХ.

где - площадь левой грани тетраэдра (площ. треугольника);

ωn – площадь nй грани тетраэдра;

X – проекция единичной массовой силы, действующей на единицу массы тетраэдра (если действует только сила тяжести, то это проекция ускорения свободного падения);

– объём тетраэдра.

Т.о. масса тетраэдра , и проекция массовых сил, действующих на тетраэдр: .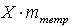

- это проекция площади грани тетраэдра n на плоскость YOZ. Из рассмотрения рис. 2.3 видно, что это левая грань тетраэдра, площадь которой равна: , т.е.

- проекций на OX нет

Таким образом:

Перейдем к пределу, стягивая тетраэдр в точку, тогда

а, значит:

Аналогично составив уравнения равновесия для проекций сил на OY и OZ, получим: ,

Т.е. .

При стягивании в точку силы давления равны на разных плоскостях, плоскость образовавшая грань n, была проведена произвольно (в положительном октанте лишь для удобства восприятия). Следовательно, величина силы давления не зависит от ориентации площадки, и из определения давления – и само гидростатическое давление не зависит от ориентации площадки.(Давление в покоящейся жидкости действует во все стороны одинаково)