Уравнение неразрывности

Уравнение неразрывности как для элементарной струйки, так и для всего потока - это математическое выражение условия сплошности потока при установившемся течении жидкости.

Выделим в потоке элементарную струйку (рис. 3.9).

Рассмотрим участок между сечениями 1-1 и 2-2. За время dt внутрь этого участка через сечение 1-1 войдет количество жидкости, равное объ­ему цилиндра с площадью основания dS₁ и образующей u₁dt. Через сече­ние 2-2 за это же время вытечет объем жидкости, равный u2dtdS₂. Отме­тим следующие обстоятельства:

1 через боковые поверхности элементарной струйки жидкость не про­никает (таково свойство трубки тока);

2 жидкость несжимаема и в ней отсутствуют пустоты и разрывы.

Это означает, что будет справедливым равенство и1 dt dS1= u2dtdS₂. Откуда и1 dS1= u2dS₂. (3.1)

Для других сечений будут справедливы такие же соотношения:

Это уравнение (3.1) и выражает условие неразрывности элементар­ной струйки, из него следует, что через все сечения струйки проходит оди- шковый расход жидкости. Из уравнения понятно, что т. е. скорости течения в разных сечениях элементарной струйки обратно пропорциональны площадям этих сечений.

Для полного потока уравнение неразрывности можно получить, проинтегрировав уравнение (3.1) по площадям соответствующих сечений ватного потока (рис. 3.9):

Используя понятие средней скорости по сечению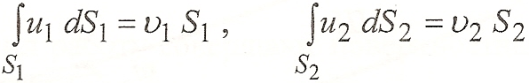

можно записать (3.2)

Так как сечения 1-1 и 2-2 выбраны произвольно, то и для любых других сечений это равенство будет справедливо.

v₁S_l=u₂S₂=v₃S₃=... = v_nS_n= const = Q. (3.3)

Уравнения (3.2) и (3.3) и есть уравнения неразрывности полного по­тока. Они показывают, что объемный расход несжимаемой жидкости при установившемся движении остается постоянным вдоль всего потока.

Из уравнения (3.2) следует, что средние скорости потока обратно пропорциональны площадям соответствующих живых сечений: